
【题目】下列命题中正确的有( )
①相等的角是对顶角.
②在同一平面内,若a∥b,b∥c,则a∥c.
③若点P(m+3,m+1)在x轴上,则点P的坐标为(4,0).
④数轴上每一个点都表示唯一一个实数.
⑤若a大于0,b不大于0,则点P(-a,-b)在第三象限.
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】分析: ①根据对顶角的定义进行判定, ②根据平行于同一条直线的两条直线平行进行判定, ③根据点在x轴上,纵坐标为0,可列方程求m,即可求出m点的坐标. ④根据数轴上的点与实数是一一对应的关系可判定, ⑤根据a大于0,确定-a是小于0,根据b不大于0,确定-b是大于等于0,再根据平面直角坐标系内点的坐标特征进行判定,坐标轴上的点不属于任何象限.
详解: ①因为对顶角是有一个公共顶点,且一个角的两边延长线是另一个角的两边,且对顶角相等,但相等的角不一定是对顶角,所以①表述错误,
②因为平行于同一条直线的两条直线平行,所以在同一平面内,若a∥b,b∥c,则a∥c,所以②表述正确,
③因为点P(m+3,m+1)在x轴上,所以m+1=0, m=-1,所以m+3=-2,则点P的坐标为(2,0),所以③表述不正确,
④因为数轴上的点与实数是一一对应的关系,所以数轴上每一个点都表示唯一一个实数,所以④表述正确,
⑤因为a大于0,b不大于0,所以![]() ,则点P(-a,-b)在第二象限或在x轴上,所以⑤表述错误,
,则点P(-a,-b)在第二象限或在x轴上,所以⑤表述错误,
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,AB∥CD,点 E 为射线 FG 上一点.
(1)如图 1,若∠EAF=30°,∠EDG=40°,则∠AED= °;
(2)如图 2,当点 E 在 FG 延长线上时,此时 CD 与 AE 交于点 H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;
(3)如图 3,DI 平分∠EDC,交 AE 于点 K,交 AI 于点 I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善住房条件,小亮的父母考察了某小区的![]() 两套楼房,
两套楼房,![]() 套楼房在第
套楼房在第![]() 层楼,
层楼,![]() 套楼房在第
套楼房在第![]() 层楼,
层楼,![]() 套楼房的面积比
套楼房的面积比![]() 套楼房的面积大24平方米,两套楼房的房价相同,第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设
套楼房的面积大24平方米,两套楼房的房价相同,第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设![]() 套楼房的面积为
套楼房的面积为![]() 平方米,
平方米,![]() 套楼房的面积为
套楼房的面积为![]() 平方米,根据以上信息列出了下列方程组.其中正确的是( ).
平方米,根据以上信息列出了下列方程组.其中正确的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.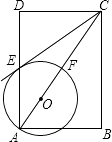
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB= ![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校住校生宿舍有大小两种寝室若干间,据统计该校高一年级男生740人,使用了55间大寝室和50间小寝室,正好住满;女生730人,使用了大寝室50间和小寝室55间,也正好住满.求该校的大小寝室每间各住多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A(0,a)、B(b, 0),且a、b满足: ![]() ,点D为x正半轴上一动点
,点D为x正半轴上一动点
(1)求A、B两点的坐标
(2)如图,∠ADO的平分线交y轴于点C,点 F为线段OD上一动点,过点F作CD的平行线交y轴于点H,且∠AFH=45°, 判断线段AH、FD、AD三者的数量关系,并予以证明

(3)以AO为腰,A为顶角顶点作等腰△ADO,若∠DBA=30°,直接写出∠DAO的度数

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com