
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.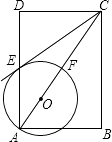
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB= ![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
【答案】
(1)解:直线CE与⊙O相切.
理由如下:
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°
∴∠AE0+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,
∴直线CE与⊙O相切.
(2)解:∵tan∠ACB= ![]() =
= ![]() ,BC=2,
,BC=2,
∴AB=BCtan∠ACB= ![]() ,
,
∴AC= ![]() ;
;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB= ![]() ,
,
∴DE=DCtan∠DCE=1;
方法一:在Rt△CDE中,CE= ![]() =
= ![]() ,
,
连接OE,设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,即 ![]() =r2+3
=r2+3
解得:r= ![]()
方法二:AE=AD﹣DE=1,过点O作OM⊥AE于点M,则AM= ![]() AE=
AE= ![]()
在Rt△AMO中,OA= ![]() =
= ![]() ÷
÷ ![]() =
= ![]()
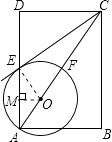
【解析】本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;(2)在直角三角形ABC中,根据三角函数的定义可以求得AB= ![]() ,然后根据勾股定理求得AC=
,然后根据勾股定理求得AC= ![]() ,同理知DE=1;方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2 , 即
,同理知DE=1;方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2 , 即 ![]() =r2+3,从而易得r的值;方法二、过点O作OM⊥AE于点M,在Rt△AMO中,根据三角函数的定义可以求得r的值.
=r2+3,从而易得r的值;方法二、过点O作OM⊥AE于点M,在Rt△AMO中,根据三角函数的定义可以求得r的值.


科目:初中数学 来源: 题型:
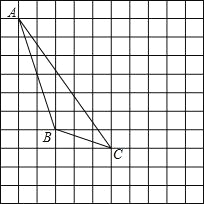
【题目】如图,每个小正方形的边长为 1 个单位,每个小方格的顶点叫格点.
(1)画出△ABC 的 AB 边上的中线 CD;
(2)画出△ABC 向右平移 4 个单位后得到的△A1B1C1;
(3)图中 AC 与 A1C1 的关系是: ;
(4)图中△ABC 的面积是 ;
(5)能使△BCE 面积为 3 的格点 E 有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
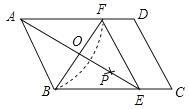
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是 ;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 ,∠ABC= °.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情系灾区.5月12日我国四川汶川县发生里氏8.0级大地震,地震给四川,甘肃,陕西等地造成巨大人员伤亡和财产损失.灾难发生后,我校师生和全国人民一道,迅速伸出支援的双手,为灾区人民捐款捐物.为了支援灾区学校灾后重建,我校决定象灾区捐助床架60个,课桌凳100套.现计划租甲、乙两种货车共8辆将这些物质运往灾区,已知一辆甲货车可装床架5个和课桌凳20套,一辆乙货车可装床架10个和课桌凳10套.
(1)学校如何安排甲、乙两种货车可一次性把这些物资运到灾区?有几种方案?
(2)若甲种货车每辆要付运输费1200元,乙种货车要付运输费1000元,则学校应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的有( )
①相等的角是对顶角.
②在同一平面内,若a∥b,b∥c,则a∥c.
③若点P(m+3,m+1)在x轴上,则点P的坐标为(4,0).
④数轴上每一个点都表示唯一一个实数.
⑤若a大于0,b不大于0,则点P(-a,-b)在第三象限.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com