
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(0,2)和B(1,
经过点A(0,2)和B(1,![]() ).
).
(1)求该抛物线的表达式;
(2)已知点C与点A关于此抛物线的对称轴对称,点D在抛物线上,且点D的横坐标为4,求点C与点D的坐标;
(3)在(2)的条件下,将抛物线在点A,D之间的部分(含点A,D)记为图象G,如果图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.
【答案】(1)y=![]() x2﹣x+2;(2)C点坐标为(2,2);D点坐标为(4,6);(3)当1<t≤3时,图象G向下平移t(t>0)个单位后与直线BC只有一个公共点.
x2﹣x+2;(2)C点坐标为(2,2);D点坐标为(4,6);(3)当1<t≤3时,图象G向下平移t(t>0)个单位后与直线BC只有一个公共点.
【解析】
试题分析:(1)把A点和B点坐标代入![]() 得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)利用配方法得到y=![]() (x﹣1)2+
(x﹣1)2+![]() ,则抛物线的对称轴为直线x=1,利用点C与点A关于直线x=1对称得到C点坐标为(2,2);然后利用二次函数图象上点的坐标特征求D点坐标;
,则抛物线的对称轴为直线x=1,利用点C与点A关于直线x=1对称得到C点坐标为(2,2);然后利用二次函数图象上点的坐标特征求D点坐标;
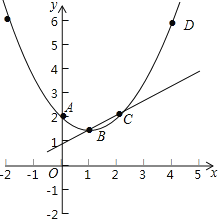
(3)画出抛物线,如图,先利用待定系数法求出直线BC的解析式为y=![]() x+1,再利用平移的性质得到图象G向下平移1个单位时,点A在直线BC上;图象G向下平移3个单位时,点D在直线BC上,由于图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,所以1<t≤3.
x+1,再利用平移的性质得到图象G向下平移1个单位时,点A在直线BC上;图象G向下平移3个单位时,点D在直线BC上,由于图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,所以1<t≤3.
解:(1)把A(0,2)和B(1,![]() )代入
)代入![]() 得
得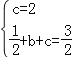 ,解得
,解得![]() ,
,
所以抛物线解析式为y=![]() x2﹣x+2;
x2﹣x+2;
(2)∵y=![]() x2﹣x+2=
x2﹣x+2=![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴抛物线的对称轴为直线x=1,
∵点C与点A关于此抛物线的对称轴对称,
∴C点坐标为(2,2);
当x=4时,y=![]() x2﹣x+2=8﹣4+2=6,
x2﹣x+2=8﹣4+2=6,
∴D点坐标为(4,6);
(3)如图,
设直线BC的解析式为y=mx+n,
把B(1,![]() ),C(2,2)代入得
),C(2,2)代入得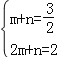 ,解得
,解得![]() ,
,
∴直线BC的解析式为y=![]() x+1,
x+1,
当x=0时,y=![]() x+1=1,
x+1=1,
∴点图象G向下平移1个单位时,点A在直线BC上,
当x=4时,y=![]() x+1=3,
x+1=3,
∴点图象G向下平移3个单位时,点D在直线BC上,
∴当1<t≤3时,图象G向下平移t(t>0)个单位后与直线BC只有一个公共点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】说明命题“等腰三角形腰上的高小于腰”是假命题的反例可以是( )
A.等腰直角三角形
B.等边三角形
C.含30°的直角三角形
D.顶角为45°的等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=x+2与双曲线![]() 相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.
相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.
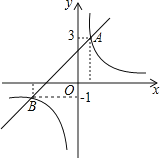
(1)求k的值;
(2)若y1<y2,请你根据图象确定x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:

(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= ;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,过点C作CE∥AD交AB于E,连接AC、DE,AC与DE交于点F.
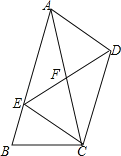
(1)求证:四边形AECD为平行四边形;
(2)如果EF=2![]() ,∠FCD=30°,∠FDC=45°,求DC的长.
,∠FCD=30°,∠FDC=45°,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
如果y′=![]() ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”
为点(﹣5,﹣6).
(1)①点(2,1)的“关联点”为 ;②如果点A(3,﹣1),B(﹣1,3)的“关联点”中有一个在函数![]() 的图象上,那么这个点是 (填“点A”或“点B”).
的图象上,那么这个点是 (填“点A”或“点B”).
(2)①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”,
那么点M的坐标为 ;②如果点N*(m+1,2)是一次函数y=x+3图象上点N的“关联点”,求点N的坐标.
(3)如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,其“关联点”Q的纵坐标
y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”为[1,m-3]的一次函数是正比例函数,则关于x的方程mx-6=0的解为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com