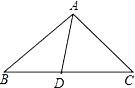
【题目】已知，如图△ABC中，AB=AC，D点在BC上，且BD=AD，DC=AC（本题6分）
（1）写出图中两个等腰三角形，
（2）求∠B的度数．
【答案】（1）△ABC，△ACD．△ABD；（2）∠B的度数为36°．
【解析】（1）根据，AB=AC，DC=AC，BD=AD可判断出等腰三角形．
（2）设∠B=x°∵BD=AD∴∠DAB=∠B=x°，利用等腰三角形的性质和三角形内角和定理即可解题．
解：（1）△ABC，△ACD．△ABD，
由 AB=AC，可得△ABC是等腰三角形；由 BD=AD，可得△ABD是等腰三角形；
由DC=AC得△ACD是等腰三角形．
（2）设∠B=x，∵BD=AD，∴∠DAB=∠B=x，
∵AB=AC，∴∠C=∠B=x，
∵DC=AC，∴∠CAD=∠ADC=∠DAB+∠B=2x，
在△ACD中，由∠CAD+∠ADC+∠C=180°，得2x+2x+x=180，
解得x=36°，∴∠B=36°．
答：∠B的度数为36°．
科目：初中数学 来源： 题型：
【题目】问题背景：
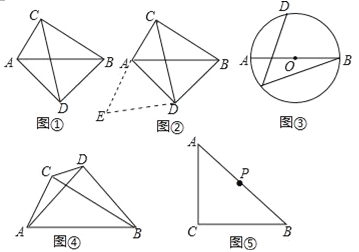
如图①，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=
CD，从而得出结论：AC+BC=CD．
简单应用：
（1）在图①中，若AC=，BC=
，则CD= ．
（2）如图③，AB是⊙O的直径，点C、D在⊙上，
，若AB=13，BC=12，求CD的长．
拓展规律：
（3）如图④，∠ACB=∠ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD的长（用含m，n的代数式表示）
（4）如图⑤，∠ACB=90°，AC=BC，点P为AB的中点，若点E满足AE=
AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，抛物线
（ a≠0）经过原点，顶点为A （ h，k ） （h≠0）．
（1）当h＝1，k＝2时，求抛物线的解析式；
（2）若抛物线
（t≠0）也经过A点，求a与t之间的关系式；
（3）当点A在抛物线
上，且－2≤h＜1时，求a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
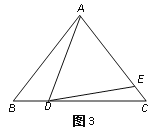
【题目】△ABC中，AB=AC.
（1）如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=_____度；
（2）如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=_______度；
（3）思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：____________________.
（4）如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知A，D，C，F在同一直线上，AB＝DE，BC＝EF，要使△ABC≌△DEF，还需添加一个条件是( )
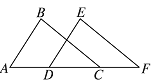
A. ∠BCA＝∠F B. ∠B＝∠E C. BC∥EF D. ∠A＝∠EDF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com