
【题目】已知,抛物线![]() ( a≠0)经过原点,顶点为A ( h,k ) (h≠0).
( a≠0)经过原点,顶点为A ( h,k ) (h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线![]() (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线![]() 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)设抛物线的解析式为:![]() ,把h=1,k=2代入得到:
,把h=1,k=2代入得到:![]() .由抛物线过原点,得到
.由抛物线过原点,得到![]() ,从而得到结论;
,从而得到结论;
(2)由抛物线![]() 经过点A(h,k),得到
经过点A(h,k),得到![]() ,从而有
,从而有![]() ,由抛物线经过原点,得到
,由抛物线经过原点,得到![]() ,从而得到
,从而得到![]() ;
;
(3)由点A(h,k)在抛物线![]() 上,得到
上,得到![]() ,故
,故![]() ,由抛物线经过原点,得到
,由抛物线经过原点,得到![]() ,从而有
,从而有![]() ;然后分两种情况讨论:①当-2≤h<0时,②当0<h<1时.
;然后分两种情况讨论:①当-2≤h<0时,②当0<h<1时.
试题解析:(1)根据题意,设抛物线的解析式为:![]() (a≠0),∵h=1,k=2,∴
(a≠0),∵h=1,k=2,∴![]() .∵抛物线过原点,∴
.∵抛物线过原点,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() ;
;
(2)∵抛物线![]() 经过点A(h,k),∴
经过点A(h,k),∴![]() ,∴
,∴![]() ,∵抛物线经过原点,∴
,∵抛物线经过原点,∴![]() ,∵h≠0,∴
,∵h≠0,∴![]() ;
;
(3)∵点A(h,k)在抛物线![]() 上,∴
上,∴![]() ,∴
,∴![]() ,∵抛物线经过原点,∴
,∵抛物线经过原点,∴![]() ,∵h≠0,∴
,∵h≠0,∴![]() ;
;
分两种情况讨论:
①当-2≤h<0时,由反比例函数性质可知:![]() ,∴
,∴![]() ;
;
②当0<h<1时,由反比例函数性质可知:![]() ,∴
,∴![]() ;
;
综上所述,a的取值范围是![]() 或
或![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
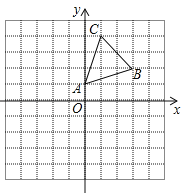
【题目】((2016甘肃省白银市)如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题不正确的是( )
A. 任何一个成中心对称的四边形是平行四边形
B. 平行四边形既是轴对称图形又是中心对称图形
C. 线段、平行四边形、矩形、菱形、正方形都是中心对称图形
D. 等边三角形、矩形、菱形、正方形都是轴对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各命题都成立,而它们的逆命题不能成立的是( ).
A.两直线平行,同位角相等 B.全等三角形的对应角相等
C.四边相等的四边形是菱形 D.直角三角形中, 斜边的平方等于两直角边的平方和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( )
A.3×106
B.3×105
C.0.3×106
D.30×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是一个严重缺水的国家,大家应加倍珍惜水资源,节约用水,据测试,拧不紧的水龙头每秒钟会滴下 2 滴水,每滴水约 0.05 毫升.小明同学在洗手后,没有把水龙头拧紧,当小明离开 4 小时后水龙头滴了约______毫升水(用科学记数法表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016江西省)设抛物线的解析式为![]() ,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点
,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点![]() (
(![]() ,0 ) (n为正整数 )作x轴的垂线,交抛物线于点
,0 ) (n为正整数 )作x轴的垂线,交抛物线于点![]() ,连接
,连接![]() ,得直角三角形
,得直角三角形![]() .
.
(1)求a的值;
(2)直接写出线段![]() ,
,![]() 的长(用含n的式子表示);
的长(用含n的式子表示);
(3)在系列Rt△![]() 中,探究下列问题:
中,探究下列问题:
①当n为何值时,Rt△![]() 是等腰直角三角形?
是等腰直角三角形?
②设1≤k<m≤n (k,m均为正整数),问是否存在Rt△![]() 与Rt△
与Rt△![]() 相似?若存在,求出其相似比;若不存在,说明理由.
相似?若存在,求出其相似比;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com