
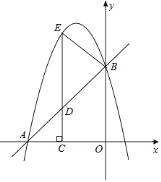
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与坐标轴分别交于
与坐标轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 过
过![]() 、
、![]() 两点,点
两点,点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 求
求![]() 面积的最大值.
面积的最大值.
![]() 连接
连接![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出点
相似?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
【答案】(1)![]() .(2)存在点
.(2)存在点![]() ,使得
,使得![]() 和
和![]() 相似,点
相似,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)首先求出点A、B的坐标,然后利用待定系数法求出抛物线的解析式;
(2)设点C坐标为(m,0)(m<0),则点E坐标为(m,-m2-3m+4),从而得出OC=-m、OF=-m2-3m+4、BF=-m2-3m,根据S△ABE=S梯形AOFE-S△AOB-S△BEF得出S=-2(m+2)2+8,据此可得答案;
(3)由于△ACD为等腰直角三角形,而△DBE和△DAC相似,则△DBE必为等腰直角三角形.分两种情况讨论,要点是求出点E的坐标,由于点E在抛物线上,则可以由此列出方程求出未知数.
![]() 在直线解析式
在直线解析式![]() 中,令
中,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
∴![]() ,
,![]() .
.
∵点![]() ,
,![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
∴抛物线的解析式为:![]() .
.
![]() 如图,连接
如图,连接![]() 、过点
、过点![]() 作
作![]() 轴于点
轴于点![]() ,
,

设点![]() 坐标为
坐标为![]() ,则点
,则点![]() 坐标为
坐标为![]() ,
,
则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
则![]()
![]() .
.
![]()
![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.
即![]() 面积的最大值为
面积的最大值为![]() .
.![]() 设点
设点![]() 坐标为
坐标为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
则![]() .
.
∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() 和
和![]() 相似
相似
∴![]() 必为等腰直角三角形.
必为等腰直角三角形.
![]() 若
若![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,解得
,解得![]() (不合题意,舍去)或
(不合题意,舍去)或![]() ,
,
∴![]() ;
;
![]() 若
若![]() ,则
,则![]() ,
,
在等腰直角三角形![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,解得
,解得![]() (不合题意,舍去)或
(不合题意,舍去)或![]() ,
,
∴![]() .
.
综上所述,存在点![]() ,使得
,使得![]() 和
和![]() 相似,点
相似,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】在某市实施城中村改造的过程中,“旺鑫”拆迁工程队承包了一项10000 m2的拆迁工程.由于准备工作充分,实际拆迁效率比原计划提高了25%,提前2天完成了任务,请解答下列问题:
(1)求“旺鑫”拆迁工程队现在平均每天拆迁多少平方米;
(2)为了尽量减少拆迁给市民带来的不便,在拆迁工作进行了2天后,“旺鑫”拆迁工程队的领导决定加快拆迁工作,将余下的拆迁任务在5天内完成,那么“旺鑫”拆迁工程队平均每天至少再多拆迁多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交,其顶点坐标为
轴正半轴相交,其顶点坐标为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有两个相等的实数根,其中正确的结论是________.(只填序号即可).
有两个相等的实数根,其中正确的结论是________.(只填序号即可).
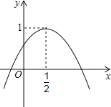
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或解方程:
(1)计算下列各题
①(π﹣3.14)0+(﹣![]() )2﹣3﹣2;
)2﹣3﹣2;
②(3a﹣1)2﹣(3a﹣2)(3a+4);
③(12a5b7﹣8a4b6﹣4a4b2)÷(﹣2a2b)2;
(2)解分式方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
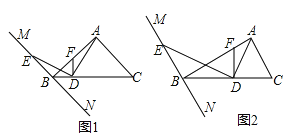
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com