
【题目】在同一平面直角坐标系中,一次函数y=kx﹣2k和二次函数y=﹣kx2+2x﹣4(k是常数且k≠0)的图象可能是( )
A. 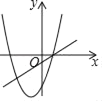 B.
B. 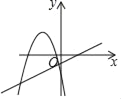
C. 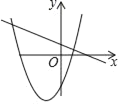 D.
D. 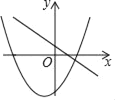
【答案】C
【解析】
根据一次函数与二次函数的图象的性质,求出k的取值范围,再逐项判断即可.
解:A、由一次函数图象可知,k>0,∴﹣k<0,∴二次函数的图象开口应该向下,故A选项不合题意;
B、由一次函数图象可知,k>0,∴﹣k<0,-![]() =
=![]() >0,∴二次函数的图象开口向下,且对称轴在x轴的正半轴,故B选项不合题意;
>0,∴二次函数的图象开口向下,且对称轴在x轴的正半轴,故B选项不合题意;
C、由一次函数图象可知,k<0,∴﹣k>0,-![]() =
=![]() <0,,∴二次函数的图象开口向上,且对称轴在x轴的负半轴,一次函数必经过点(2,0),当x=2时,二次函数值y=﹣4k>0,故C选项符合题意;
<0,,∴二次函数的图象开口向上,且对称轴在x轴的负半轴,一次函数必经过点(2,0),当x=2时,二次函数值y=﹣4k>0,故C选项符合题意;
D、由一次函数图象可知,k<0,∴﹣k>0,-![]() =
=![]() <0,,∴二次函数的图象开口向上,且对称轴在x轴的负半轴,一次函数必经过点(2,0),当x=2时,二次函数值y=﹣4k>0,故D选项不合题意;
<0,,∴二次函数的图象开口向上,且对称轴在x轴的负半轴,一次函数必经过点(2,0),当x=2时,二次函数值y=﹣4k>0,故D选项不合题意;
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】当你站在博物馆的展览厅中时,你知道站在何处观赏最理想吗?如图,设墙壁上的展品最高点P距地面2.5米,最低点Q距地面2米,观赏者的眼睛F距地面1.6米,当视角∠PEQ最大时,站在此处观赏最理想,则此时E到墙壁的距离为( )米.

A. 1 B. 0.6 C. 0.5 D. 0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆客房部有![]() 个房间供游客居住,当每个房间的定价为每天
个房间供游客居住,当每个房间的定价为每天![]() 元时,所有房间刚好可以住满,根据经验发现,每个房间的定价每增加
元时,所有房间刚好可以住满,根据经验发现,每个房间的定价每增加![]() 元,就会有
元,就会有![]() 个房间空闲,对有游客入住的房间,宾馆需对每个房间支出每天
个房间空闲,对有游客入住的房间,宾馆需对每个房间支出每天![]() 元的各种费用.设每个房间的定价增加
元的各种费用.设每个房间的定价增加![]() 元,每天的入住量为
元,每天的入住量为![]() 个,客房部每天的利润为
个,客房部每天的利润为![]() 元.
元.
![]() 求
求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 求
求![]() 与
与![]() 的函数关系式,并求客房部每天的最大利润是多少?
的函数关系式,并求客房部每天的最大利润是多少?
![]() 当
当![]() 为何值时,客房部每天的利润不低于
为何值时,客房部每天的利润不低于![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD的边BC的延长线上取一点E,在直线BC的同侧作一个以CE为底的等腰△CEF,且满足∠B+∠F=180°,则称三角形CEF为四边形ABCD的“伴随三角形”.
(1)如图1,若△CEF是正方形ABCD的“伴随三角形”:
①连接AC,则∠ACF= ;
②若CE=2BC,连接AE交CF于H,求证:H是CF的中点;
(2)如图2,若△CEF是菱形ABCD的“伴随三角形”,∠B=60°,M是线段AE的中点,连接DM、FM,猜想并证明DM与FM的位置与数量关系.
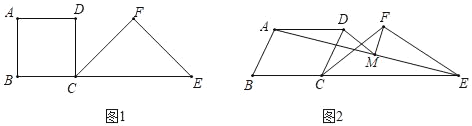
查看答案和解析>>
科目:初中数学 来源: 题型:
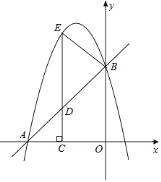
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与坐标轴分别交于
与坐标轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 过
过![]() 、
、![]() 两点,点
两点,点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 求
求![]() 面积的最大值.
面积的最大值.
![]() 连接
连接![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出点
相似?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
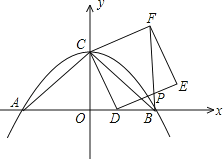
【题目】如图,抛物线y=﹣![]() x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.
x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.
(1)试判断△ABC的形状,并说明理由;
(2)求证:BF⊥AB.
(3)当点D从点O沿x轴正方向移动到点B时,点E所走过的路线长为______;
(4)探究当点D在何处时,△FBC是等腰三角形,并求出相应的BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①两条对角线相等的四边形是矩形;②有一组对边相等,一组对角是直角的四边形是矩形;③有一个角为直角,两条对角线相等的四边形是矩形;④四个角都相等的四边形是矩形⑤相邻两边都互相垂直的四边形是矩形.其中判断正确的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
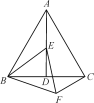
(1)求证:AE=CF;
(2)求∠ACF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com