
【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
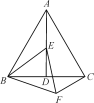
(1)求证:AE=CF;
(2)求∠ACF的度数.
【答案】(1)证明见解析;(2)∠ACF=90°.
【解析】
(1)根据△ABC是等边三角形,得出AB=BC,∠ABE+∠EBC=60°,再根据△BEF是等边三角形,得出EB=BF,∠CBF+∠EBC=60°,从而求出∠ABE=∠CBF,最后根据SAS证出△ABE≌△CBF,即可得出AE=CF;
(2)根据△ABC是等边三角形,AD是∠BAC的角平分线,得出∠BAE=30°,∠ACB=60°,再根据△ABE≌△CBF,得出∠BCF=∠BAE=30°,从而求出∠ACF的度数.
(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABE+∠EBC=60 °.
∵△BEF是等边三角形,
∴EB=BF,∠CBF+∠EBC=60 °.
∴∠ABE=∠CBF.
在△ABE和△CBF中,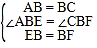 ,
,
∴△ABE≌△CBF(SAS).
∴AE=CF;
(2)∵等边△ABC中,AD是∠BAC的角平分线,
∴∠BAE=![]() ∠BAC=30 °,∠ACB=60°.
∠BAC=30 °,∠ACB=60°.
∵△ABE≌△CBF,
∴∠BCF=∠BAE=30 °.
∴∠ACF=∠BCF+∠ACB=30 °+60 °=90 °.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)将![]() 向上平移
向上平移![]() 个单位长度,再向左平移
个单位长度,再向左平移![]() 个单位长度,得到
个单位长度,得到![]() ,请画出
,请画出![]() (点
(点![]() ,
,![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ,
,![]() )
)
(2)请画出与![]() 关于
关于![]() 轴对称的
轴对称的![]() (点
(点![]() ,
,![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ,
,![]() )
)
(3)请写出![]() ,
,![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
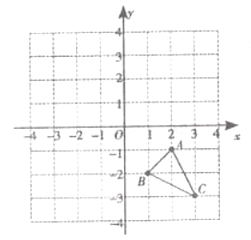
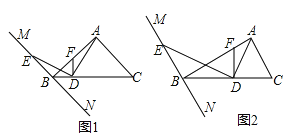
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
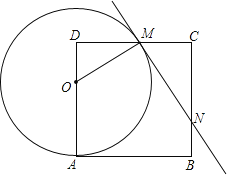
(1)图中是否存在与△ODM相似的三角形,若存在,请找出并给予证明;
(2)设DM=x,OA=R,求R关于x的函数关系式;
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
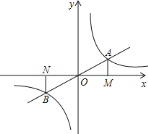
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 在第一象限的图象交于
在第一象限的图象交于![]() 点,过
点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,已知
,已知![]() 的面积为
的面积为![]() .
.
![]() 求反比例函数的解析式;
求反比例函数的解析式;
![]() 如图,点
如图,点![]() 为反比例函数在第三象限图象上的点,过
为反比例函数在第三象限图象上的点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
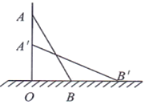
【题目】如图,一架云梯AB长25分米,斜靠在一面墙上,梯子底端B离墙7分米.
(1)这个梯子的顶端A距地面有多高?
(2)如果梯子顶端下滑了4分米,那么梯子的底端在水平方向滑动了多少分米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com