
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуOЃЈ0ЃЌ0ЃЉЃЌAЃЈЃ5ЃЌ0ЃЉЃЌBЃЈ2ЃЌ1ЃЉЃЌХзЮяЯпlЃКyЃНЃЃЈxЃhЃЉ2ЃЋ1ЃЈhЮЊГЃЪ§ЃЉгыyжсЕФНЛЕуЮЊCЃЎ

ЃЈ1ЃЉlОЙ§ЕуBЃЌЧѓЫќЕФНтЮіЪНЃЌВЂаДГіДЫЪБlЕФЖдГЦжсМАЖЅЕузјБъЃК
ЃЈ2ЃЉЩшЕуCЕФзнзјБъЮЊycЃЌЧѓycЕФзюДѓжЕЃЌДЫЪБlЩЯгаСНЕуЃЈx1ЃЌy1ЃЉЃЌЃЈx2ЃЌy2ЃЉЃЌЦфжаx1ЃОx2Ён0ЃЌБШНЯy1гыy1ЕФДѓаЁЃЛ
ЃЈ3ЃЉЕБЯпЖЮOAБЛlжЛЗжЮЊСНВПЗжЃЌЧветСНВПЗжЕФБШЪЧ1ЃК4ЪБЃЌЧѓhЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЖдГЦжсxЃН2ЃЌЖЅЕуBЃЈ2ЃЌlЃЉЃЛЃЈ2ЃЉy1ЃМy1ЃЛЃЈ3ЃЉhЃН0ЛђhЃНЃ5ЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉНЋЕуBДњШыХзЮяЯпЕФНтЮіЪНЃЌЕУНтЮіЪНЃЌДгЖјЕУЕНХзЮяЯпЕФЖдГЦжсМАЖЅЕузјБъЃЛ
ЃЈ2ЃЉгУКЌhЕФЪНзгБэЪОyCЃЌдкИљОнЪНзгЬиЕуЧѓГіyCЕФзюДѓжЕМАДЫЪБЕФhжЕЃЌДЫЪБдйХаЖЯlдкxЃО0ЪБЕФдіМѕад;
ЃЈ3ЃЉЩшlгыxжсЕФНЛЕуЮЊMЃЌдђOM=ЃЈ1/5ЃЉOAЛђAM=ЃЈ1/5ЃЉOAЃЌНјЖјЕУЕНMЕФзјБъЃЌДњШыНтЮіЪНЃЌЧѓЕУhЕФжЕЃЎ
ЪдЬтНтЮіЃК
НтЃКЃЈlЃЉАбxЃН2ЃЌyЃН1ДњШыyЃНЃЃЈxЃhЃЉ2ЃЋ1ЃЌЕУhЃН2ЃЎ
ЁрНтЮіЪНЮЊyЃНЃЃЈxЃ2ЃЉ2ЃЋ1ЃЈЛђyЃНЃx2ЃЋ4xЃ3ЃЉЃЎ
ЖдГЦжсxЃН2ЃЌЖЅЕуBЃЈ2ЃЌlЃЉЃЎ
ЃЈ2ЃЉЕуCЕФКсзјБъЮЊ0ЃЌдђyCЃНЃh2ЃЋ1ЃЌ
ЁрЕБhЃН0ЪБЃЌyCгазюДѓжЕЮЊ1ЃЎ
ДЫЪБЃЌlЮЊyЃНЃx2ЃЋ1ЃЌЖдГЦжсЮЊyжсЃЌЕБxЁн0ЪБЃЌyЫцзХxЕФдіДѓЖјМѕаЁЃЎ
Ёрx1ЃОx2Ён0ЪБЃЌy1ЃМy1ЃЎ
ЃЈ3ЃЉАбOAЗж1ЃК4СНВПЗжЕФЕуЮЊЃЈЃ1ЃЌ0ЃЉЛђЃЈЃ4ЃЎ0ЃЉЃЎ
ЂйxЃН-1ЃЌyЃН0ДњШыyЃНЃЃЈxЃhЃЉ2ЃЋ1ЃЌЕУhЃН0ЛђhЃНЃ2ЃЎ
ЕЋhЃНЃ2ЪБЃЌOAБЛЗжЮЊШ§ВПЗжЃЌВЛКЯЬтвтЃЌЩсШЅЃЎ
ЂкЭЌбљЃЌАбxЃНЃ4ЃЌyЃН0ДњШыyЃНЃЃЈxЃhЃЉ2ЃЋ1ЃЌЕУhЃНЃ5ЛђhЃНЃ3ЃЈЩсШЅЃЉ
ЁрhЃН0ЛђhЃНЃ5ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃОйааЭМЪщНквхТєЛюЖЏЃЌНЋЫљЪлПюЯюОшИјЦфЫћЦЖРЇбЇЩњЃЎдкетДЮвхТєЛюЖЏжаЃЌФГАрМЖЪлЪщЧщПіШчЯТЭМЃК
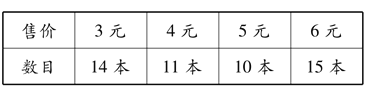
ЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.ИУАрМЖЫљЪлЭМЪщЕФзмЪ§ЪеШыЪЧ226дЊ
B.дкИУАрМЖЫљЪлЭМЪщМлИёзщГЩЕФвЛзщЪ§ОнжаЃЌжаЮЛЪ§ЪЧ4
C.дкИУАрМЖЫљЪлЭМЪщМлИёзщГЩЕФвЛзщЪ§ОнжаЃЌжкЪ§ЪЧ15
D.дкИУАрМЖЫљЪлЭМЪщМлИёзщГЩЕФвЛзщЪ§ОнжаЃЌЗНВюЪЧ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
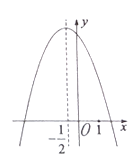
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌЖдГЦжсЮЊ
ЕФЭМЯѓШчЭМЫљЪОЃЌЖдГЦжсЮЊ![]() ЃЎЯТСаНсТлжаЃЌе§ШЗЕФЪЧ( )
ЃЎЯТСаНсТлжаЃЌе§ШЗЕФЪЧ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
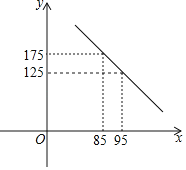
ЁОЬтФПЁПЮфККЁАаТЙкЗЮбзЁБЗЂЩњвдРДЃЌФГвНСЦЙЋЫОЛ§МЋИДЙЄЃЌМгАрМгЕуЩњВњвНгУЗРЛЄЗўЃЌЮЊЗРПивЛЯпжњСІЃЎвдЯТЪЧИУЙЋЫОвдЭљЕФЪаГЁЕїВщЃЌЗЂЯжИУЙЋЫОЗРЛЄЗўЕФШеЯњЪлСПyЃЈЬзЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфТњзувЛДЮКЏЪ§ЙиЯЕЃЌШчЯТЭМЫљЪОЃЌЙигкШеЯњЪлРћШѓwЃЈдЊЃЉКЭЯњЪлЕЅМлxЃЈдЊЃЉЕФМИзщЖдгІжЕШчЯТБэЃК
ЯњЪлЕЅМлxЃЈдЊЃЉ | 85 | 95 | 105 |
ШеЯњЪлРћШѓwЃЈдЊЃЉ | 875 | 1875 | 1875 |
ЃЈзЂЃКШеЯњЪлРћШѓЃНШеЯњЪлСПЁСЃЈЯњЪлЕЅМлвЛГЩБОЕЅМлЃЉЃЉ
ЃЈ1ЃЉЧѓyЙигкxЕФКЏЪ§НтЮіЪНЃЈВЛвЊЧѓаДГіxЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓКЭБэИёЫљЬсЙЉЕФаХЯЂЃЌЬюПеЃК
ИУЙЋЫОЩњВњЕФЗРЛЄЗўЕФГЩБОЕЅМлЪЧЁЁ ЁЁдЊЃЌЕБЯњЪлЕЅМлxЃНЁЁ ЁЁдЊЪБЃЌШеЯњЪлРћШѓwзюДѓЃЌзюДѓжЕЪЧЁЁ ЁЁдЊЃЛ
ЃЈ3ЃЉИУЙЋЫОИДЙЄвдКѓЃЌдкеўИЎВПУХЕФАяжњЯТЃЌдВФСЯВЩЙКГЩБОБШвдЭљгаСЫЯТНЕЃЌЦНОљЦ№РДЃЌУПЩњВњвЛЬзЗРЛЄЗўЃЌГЩБОБШвдЧАЯТНЕ5дЊЃЎИУЙЋЫОМЦЛЎПЊеЙПЦММДДаТЃЌвдНЕЕЭИУВњЦЗЕФГЩБОЃЌШчЙћдкНёКѓЕФЯњЪлжаЃЌШеЯњЪлСПгыЯњЪлЕЅМлШдДцдкЃЈ1ЃЉжаЕФЙиЯЕЃЎШєЯыЪЕЯжЯњЪлЕЅМлЮЊ90дЊЪБЃЌШеЯњЪлРћШѓВЛЕЭгк3750дЊЕФЯњЪлФПБъЃЌИУВњЦЗЕФГЩБОЕЅМлгІВЛГЌЙ§ЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
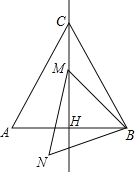
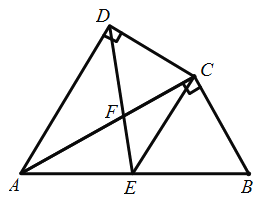
ЁОЬтФПЁПШчЭМЃЌЕШБпШ§НЧаЮABCЕФБпГЄЪЧ2ЃЌMЪЧИпCHЫљдкжБЯпЩЯЕФвЛИіЖЏЕуЃЌСЌНгMBЃЌНЋЯпЖЮBMШЦЕуBФцЪБеыа§зЊ60ЁуЕУЕНBNЃЌСЌНгMNЃЌдђдкЕуMдЫЖЏЙ§ГЬжаЃЌЯпЖЮMNГЄЖШЕФзюаЁжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОнЪаГЁЕїВщЃЌЬьУЈГЌЪадкЯњЪлвЛжжНјМлЮЊУПМў40дЊЕФЛЄблЬЈЕЦжаЗЂЯжЃКУПдТЯњЪлСП![]() ЃЈМўЃЉгыЯњЪлЕЅМл
ЃЈМўЃЉгыЯњЪлЕЅМл![]() ЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
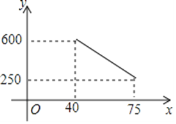
ЃЈ1ЃЉЕБЯњЪлЕЅМлЖЈЮЊ50дЊЪБЃЌЧѓУПдТЕФЯњЪлМўЪ§ЃЛ
ЃЈ2ЃЉЩшУПдТЛёЕУРћШѓЮЊ![]() ЃЈдЊЃЉЃЌЧѓУПдТЛёЕУРћШѓ
ЃЈдЊЃЉЃЌЧѓУПдТЛёЕУРћШѓ![]() ЃЈдЊЃЉЙигкЯњЪлЕЅМл
ЃЈдЊЃЉЙигкЯњЪлЕЅМл![]() ЃЈдЊЃЉЕФКЏЪ§НтЮіЪНЃЛ
ЃЈдЊЃЉЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉгЩгкЪаГЁОКељМЄСвЃЌетжжЛЄблЕЦЕФЯњЪлЕЅМлВЛЕУИпгк75дЊЃЌШчЙћвЊУПдТЛёЕУЕФРћШѓВЛЕЭгк8000дЊЃЌФЧУДУПдТЕФГЩБОзюЩйашвЊЖрЩйдЊЃПЃЈГЩБО=НјМлЁСЯњЪлСПЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
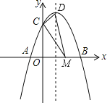
ЁОЬтФПЁПШчЭМЃЌЖдГЦжсЮЊ![]() ЕФХзЮяЯп
ЕФХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгк
жсНЛгк![]() ЕуЃЌЦфжа
ЕуЃЌЦфжа![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() ЩшХзЮяЯпЕФЖЅЕуЮЊ
ЩшХзЮяЯпЕФЖЅЕуЮЊ![]() ЃЎ
ЃЎ
![]() ЧѓХзЮяЯпЕФНтЮіЪНМАЖЅЕузјБъЃЛ
ЧѓХзЮяЯпЕФНтЮіЪНМАЖЅЕузјБъЃЛ
![]() ЮЊ
ЮЊ![]() жсЩЯЕФвЛЕуЃЌЕБ
жсЩЯЕФвЛЕуЃЌЕБ![]() ЕФжмГЄзюаЁЪБЃЌЧѓЕу
ЕФжмГЄзюаЁЪБЃЌЧѓЕу![]() ЕФзјБъМА
ЕФзјБъМА![]() ЕФжмГЄЃЎ
ЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cЕФЖЅЕуЮЊCЃЈ0ЃЌ![]() ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЧвAЃЈЉ1ЃЌ0ЃЉЃЎ
ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЧвAЃЈЉ1ЃЌ0ЃЉЃЎ
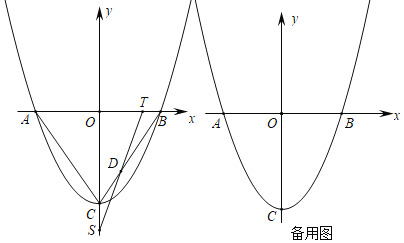
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPДгЕуBГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђЕуAдЫЖЏЃЌЭЌЪБЕуQДгЕуCГіЗЂЃЌвдУПУыvИіЕЅЮЛЕФЫйЖШЯђyжсИКЗНЯђдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЌСЌНгPQНЛЩфЯпBCгкЕуDЃЌЕБЕуPЕНДяЕуAЪБЃЌЕуQЭЃжЙдЫЖЏЃЌвдЕуPЮЊдВаФЃЌPBЮЊАыОЖЕФдВгыЩфЯпBCНЛгкЕуEЃЎ
ЂйЧѓBEЕФГЄЃЛЕБtЃН1ЪБЃЌЧѓDEЕФГЄЃЛ
ЂкШєдкЕуPЃЌQдЫЖЏЕФЙ§ГЬжаЃЌЯпЖЮDEЕФГЄЪМжеЪЧвЛИіЖЈжЕЃЌЧѓvЕФжЕМАDEГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com