
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cЕФЖЅЕуЮЊCЃЈ0ЃЌ![]() ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЧвAЃЈЉ1ЃЌ0ЃЉЃЎ
ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЧвAЃЈЉ1ЃЌ0ЃЉЃЎ
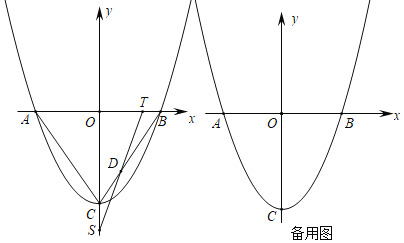
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPДгЕуBГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђЕуAдЫЖЏЃЌЭЌЪБЕуQДгЕуCГіЗЂЃЌвдУПУыvИіЕЅЮЛЕФЫйЖШЯђyжсИКЗНЯђдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЌСЌНгPQНЛЩфЯпBCгкЕуDЃЌЕБЕуPЕНДяЕуAЪБЃЌЕуQЭЃжЙдЫЖЏЃЌвдЕуPЮЊдВаФЃЌPBЮЊАыОЖЕФдВгыЩфЯпBCНЛгкЕуEЃЎ
ЂйЧѓBEЕФГЄЃЛЕБtЃН1ЪБЃЌЧѓDEЕФГЄЃЛ
ЂкШєдкЕуPЃЌQдЫЖЏЕФЙ§ГЬжаЃЌЯпЖЮDEЕФГЄЪМжеЪЧвЛИіЖЈжЕЃЌЧѓvЕФжЕМАDEГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() x2Љ
x2Љ![]() ЃЛЃЈ2ЃЉЂйЕБtЃН1ЪБЃЌ DEЃН1ЮЊЖЈжЕЃЛЂкдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌvЃН
ЃЛЃЈ2ЃЉЂйЕБtЃН1ЪБЃЌ DEЃН1ЮЊЖЈжЕЃЛЂкдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌvЃН![]() ЃЌЯпЖЮDEЕФГЄЪЧЖЈжЕ1ЃЎ
ЃЌЯпЖЮDEЕФГЄЪЧЖЈжЕ1ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩХзЮяЯпy=ax2+bx+cЕФЖЅЕуЮЊCЃЈ0ЃЌ-![]() ЃЉЃЌПЩЕУЖдГЦжсЃЌНЋХзЮяЯпНтЮіЪНИФЮЊЖЅЕуЪНЃЌНЋAЃЈ-1ЃЌ0ЃЉДњШыМДПЩЃЛ
ЃЉЃЌПЩЕУЖдГЦжсЃЌНЋХзЮяЯпНтЮіЪНИФЮЊЖЅЕуЪНЃЌНЋAЃЈ-1ЃЌ0ЃЉДњШыМДПЩЃЛ
ЃЈ2ЃЉСЌНгPEЃЌЙ§DзїDЁЭyжсгкHЃЌЩшDH=aЃЌЩшОЙ§tУыЪБЃЌЂйЕБ0ЃМtЃМ1ЪБЃЌРћгУЁїQDHЁзЁїQPOМДПЩЕУDEЕФГЄгыtЮоЙиЃЌЮЊЖЈжЕЃЛЕБt=1ЪБЃЌвзЕУDE=CE=![]() BC=1ЮЊЖЈжЕЃЛЂкЕБ1ЃМtЁм2ЪБЃЌЁїQDHЁзЁїQPOЃЌПЩЕУDEЮЊЖЈжЕЃЎ
BC=1ЮЊЖЈжЕЃЛЂкЕБ1ЃМtЁм2ЪБЃЌЁїQDHЁзЁїQPOЃЌПЩЕУDEЮЊЖЈжЕЃЎ
ЃЈ1ЃЉЁпХзЮяЯпyЃНax2+bx+cЕФЖЅЕуЮЊCЃЈ0ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЪЧyжсЃЌ
ЁрbЃН0ЃЌ
ЩшХзЮяЯпЕФНтЮіЪНЮЊyЃНax2Љ![]() ЃЌАбAЃЈЉ1ЃЌ0ЃЉДњШыyЃНax2Љ
ЃЌАбAЃЈЉ1ЃЌ0ЃЉДњШыyЃНax2Љ![]() ЃЌЕУaЃН
ЃЌЕУaЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃН![]() x2Љ
x2Љ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНгPEЃЌЙ§DзїDЁЭyжсгкHЃЌЩшDHЃНaЃЌ
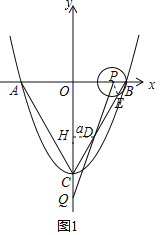
ЩшОЙ§tУыЪБЃЌPBЃНtЃЌCQЃНvtЃЌ
ЂйЕБ0ЃМtЃМ1ЪБЃЌ
ЁпPBЃНPEЃНtЃЌЁЯPBEЃН60ЁуЃЌ
ЁрЁїPBEЪЧЕШБпШ§НЧаЮЃЌ
ЁрBEЃНPBЃНtЃЛ
гж OPЃН1ЉtЃЌCQЃНvtЃЌQHЃНHC+CQЃНvt+![]() aЃЌQOЃНOC+CQЃНvt+
aЃЌQOЃНOC+CQЃНvt+![]() ЃЌ
ЃЌ
ЁпЁїQDHЁзЁїQPOЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрaЃН![]() ЃЌ
ЃЌ
ЁрDCЃН2DHЃН![]() ЃЌ
ЃЌ
ЁрDEЃНCBЉEBЉDCЃН2ЉtЉ![]() ЃН
ЃН![]() t+
t+![]() ЃЌ
ЃЌ
вРЬтвтЃЌDEЮЊЖЈжЕЃЌЙЪЕБvЃН![]() ЪБЃЌDEЕФГЄгыtЮоЙиЃЌМДDEЃН1ЃЛ
ЪБЃЌDEЕФГЄгыtЮоЙиЃЌМДDEЃН1ЃЛ
ЕБtЃН1ЪБЃЌPЕНOЕуЃЌCгыDжиКЯЃЌЯдШЛDEЃНCEЃН![]() BCЃН1ЮЊЖЈжЕЃЛ
BCЃН1ЮЊЖЈжЕЃЛ
ЂкШчЭМ2ЃЌЕБ1ЃМtЁм2ЪБЃЌOPЃНPBЉOBЃНtЉ1ЃЌ
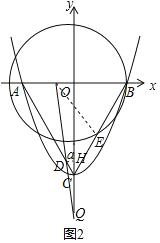
ЁпDHЃНaЃЌCHЃН![]() aЃЌQHЃНCQЉCHЃНvtЉ
aЃЌQHЃНCQЉCHЃНvtЉ![]() aЃЌQOЃНCQ+OCЃНvt+
aЃЌQOЃНCQ+OCЃНvt+![]() ЃЌ
ЃЌ
ЭЌРэЃЌЁїQDHЁзЁїQPOЃЌЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрaЃН![]() ЃЌ
ЃЌ
ЁрDCЃН2DHЃН![]() ЃЌ
ЃЌ
ЁрDEЃНDC+CEЃН![]() +ЃЈ2ЉtЃЉЃН
+ЃЈ2ЉtЃЉЃН![]() t+
t+![]() ЃЌ
ЃЌ
вРЬтвтЃЌDEЮЊЖЈжЕЃЌЙЪЕБvЃН![]() ЪБЃЌDEЃН1ЃЌ
ЪБЃЌDEЃН1ЃЌ
злЩЯЫљЪіЃЌдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌvЃН![]() ЃЌЯпЖЮDEЕФГЄЪЧЖЈжЕ1ЃЎ
ЃЌЯпЖЮDEЕФГЄЪЧЖЈжЕ1ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуOЃЈ0ЃЌ0ЃЉЃЌAЃЈЃ5ЃЌ0ЃЉЃЌBЃЈ2ЃЌ1ЃЉЃЌХзЮяЯпlЃКyЃНЃЃЈxЃhЃЉ2ЃЋ1ЃЈhЮЊГЃЪ§ЃЉгыyжсЕФНЛЕуЮЊCЃЎ

ЃЈ1ЃЉlОЙ§ЕуBЃЌЧѓЫќЕФНтЮіЪНЃЌВЂаДГіДЫЪБlЕФЖдГЦжсМАЖЅЕузјБъЃК
ЃЈ2ЃЉЩшЕуCЕФзнзјБъЮЊycЃЌЧѓycЕФзюДѓжЕЃЌДЫЪБlЩЯгаСНЕуЃЈx1ЃЌy1ЃЉЃЌЃЈx2ЃЌy2ЃЉЃЌЦфжаx1ЃОx2Ён0ЃЌБШНЯy1гыy1ЕФДѓаЁЃЛ
ЃЈ3ЃЉЕБЯпЖЮOAБЛlжЛЗжЮЊСНВПЗжЃЌЧветСНВПЗжЕФБШЪЧ1ЃК4ЪБЃЌЧѓhЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
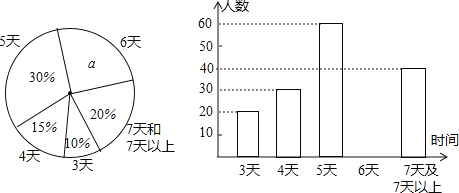
ЁОЬтФПЁПЭШЪЪаНЬг§ОжЮЊСЫСЫНтЦпФъМЖбЇЩњКЎМйВЮМгЩчЛсЪЕМљЛюЖЏЕФЬьЪ§ЃЌЫцЛњГщВщБОЪаВПЗжЦпФъМЖбЇЩњКЎМйВЮМгЩчЛсЪЕМљЛюЖЏЕФЬьЪ§ЃЌВЂгУЕУЕНЕФЪ§ОнЛцжЦСЫЯТУцСНЗљВЛЭъећЕФЭГМЦЭМЃЈШчЭМЃЉЃЎЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉaЃНЁЁ ЁЁ%ЃЌВЂаДГіИУЩШаЮЫљЖддВаФНЧЕФЖШЪ§ЮЊЁЁ ЁЁЃЛВЙШЋЬѕаЮЭМЃЛ
ЃЈ2ЃЉдкетДЮГщбљЕїВщжаЃЌвЛЙВЕїВщСЫЖрЩйУћбЇЩњЃП
ЃЈ3ЃЉШчЙћИУЪагаЦпФъМЖбЇЩњ20000ШЫЃЌЧыФуЙРМЦЁАЛюЖЏЪБМфВЛЩйгк5ЬьЁБЕФДѓдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌBDЮЊЁїABCЭтНгдВЁбOЕФжБОЖЃЌЧвЁЯBAE=ЁЯCЃЎ
ЃЈ1ЃЉЧѓжЄЃКAEгыЁбOЯрЧагкЕуAЃЛ
ЃЈ2ЃЉШєAEЁЮBCЃЌBC=2![]() ЃЌAC=2
ЃЌAC=2![]() ЃЌЧѓADЕФГЄЃЎ
ЃЌЧѓADЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
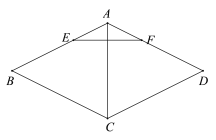
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌACЮЊЖдНЧЯпЃЌЕуEЃЌFЗжБ№дкABЃЌADЩЯЃЌBE=DFЃЌСЌНгEFЃЎ
ЃЈ1ЃЉЧѓжЄЃКACЁЭEFЃЛ
ЃЈ2ЃЉбгГЄEFНЛCDЕФбгГЄЯпгкЕуGЃЌСЌНгBDНЛACгкЕуOЃЌШєBD=4ЃЌtanG=![]() ЃЌЧѓAOЕФГЄЃЎ
ЃЌЧѓAOЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
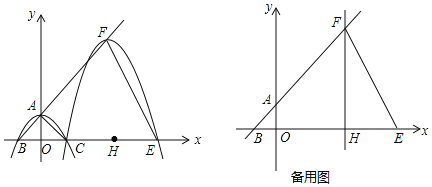
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+cЃЈaЁй0ЃЉгыyжсНЛгкЕуAЃЌгыxжсНЛгкBЁЂCСНЕуЃЈЕуCдкxжсе§АыжсЩЯЃЉЃЌЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌЧвУцЛ§ЮЊ4ЃЎЯжНЋХзЮяЯпбиBAЗНЯђЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпОЙ§ЕуCЪБЃЌгыxжсЕФСэвЛНЛЕуЮЊEЃЌЦфЖЅЕуЮЊFЃЌЖдГЦжсгыxжсЕФНЛЕуЮЊHЃЎ
ЃЈ1ЃЉЧѓaЁЂcЕФжЕЃЛ
ЃЈ2ЃЉСЌНгOFЃЌЧѓЁїOEFЕФжмГЄЃЛ
ЃЈ3ЃЉЯжНЋвЛзуЙЛДѓЕФШ§НЧАхЕФжБНЧЖЅЕуQЗХдкЩфЯпHFЩЯЃЌвЛжБНЧБпЪМжеЙ§ЕуEЃЌСэвЛжБНЧБпгыyжсЯрНЛгкЕуPЃЌЪЧЗёДцдкетбљЕФЕуQЃЌЪЙЕУвдЕуPЁЂQЁЂEЮЊЖЅЕуЕФШ§НЧаЮгыЁїPOEШЋЕШЃПШєДцдкЃЌЧыжБНгаДГіQЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
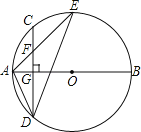
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвCDЁЭABгкЕуGЃЌЕуFЪЧCDЩЯвЛЕуЃЌЧвТњзу![]() ЃЌСЌНгAFВЂбгГЄНЛЁбOгкЕуEЃЌСЌНгADЁЂDEЃЌШєCF=2ЃЌAF=3ЃЎИјГіЯТСаНсТлЃКЂйЁїADFЁзЁїAEDЃЛЂкFG=2ЃЛЂлtanЁЯE=
ЃЌСЌНгAFВЂбгГЄНЛЁбOгкЕуEЃЌСЌНгADЁЂDEЃЌШєCF=2ЃЌAF=3ЃЎИјГіЯТСаНсТлЃКЂйЁїADFЁзЁїAEDЃЛЂкFG=2ЃЛЂлtanЁЯE=![]() ЃЛЂмSЁїDEF=4
ЃЛЂмSЁїDEF=4![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФЪЧЁЁ ЁЁЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгЩ6ИіаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌвѕгАВПЗжЪЧЭПКк2ИіаЁе§ЗНаЮЫљаЮГЩЕФЭМАИЃЎ
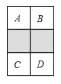
ЃЈ1ЃЉШчЙћНЋвЛСЃУзЫцЛњЕиХздкетИіЭјИёЩЯЃЌФЧУДУзСЃТфдквѕгАВПЗжЕФИХТЪЪЧ______ЃЎ
ЃЈ2ЃЉЯжНЋЭјИёФкПеАзЕФаЁе§ЗНаЮЃЈ![]() ЃЉжаШЮШЁ2ИіЭПКкЃЌЕУЕНаТЭМАИЃЎЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓаТЭМАИЪЧжсЖдГЦЭМаЮЕФИХТЪЃЎ
ЃЉжаШЮШЁ2ИіЭПКкЃЌЕУЕНаТЭМАИЃЎЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓаТЭМАИЪЧжсЖдГЦЭМаЮЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈВЛе§ШЗЕФЪЧЃЈ ЃЉ
A.ЮЊСЫНтШЋЪажааЁбЇЩњЖдЭјТчжБВЅПЮЕФТњвтГЬЖШЃЌгІВЩгУГщбљЕїВщ
B.Ъ§Он![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЗНВюЮЊ
ЕФЗНВюЮЊ![]()
C.Ш§НЧаЮЕФЕФФкаФЕНШ§НЧаЮШ§БпОрРыЯрЕШ
D.ЫГДЮСЌНгЖдНЧЯпДЙжБЕФЫФБпаЮЕФжаЕуЃЌЫљаЮГЩЕФЫФБпаЮЮЊСтаЮ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com