
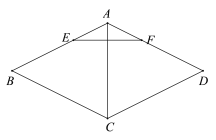
【题目】如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连接EF.
(1)求证:AC⊥EF;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O,若BD=4,tanG=![]() ,求AO的长.
,求AO的长.
【答案】(1)证明见解析;(2)AO=1。
【解析】
(1)由菱形的性质得出AB=AD,AC平分∠BAD,再根据等腰三角形的三线合一即可;
(2)根据菱形的性质和已知条件得出四边形EBDG为平行四边形,得出∠G=∠ABD,再根据tanG=![]() 即可求出AO的长.
即可求出AO的长.
(1)证明:∵四边形ABCD为菱形 ∴AB=AD,AC平分∠BAD
∵BE=DF, ∴![]() , ∴AE=AF
, ∴AE=AF
∴△AEF是等腰三角形, ∵AC平分∠BAD, ∴AC⊥EF
(2)解:如图2所示:
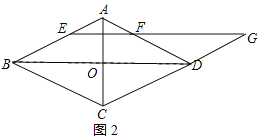
∵四边形ABCD为菱形,∴CG∥AB,BO=![]() BD=2,∵EF∥BD
BD=2,∵EF∥BD
∴四边形EBDG为平行四边形,∴∠G=∠ABD,∴tan∠ABD=tan∠G=![]()
∴tan∠ABD=![]() ,∴AO=1
,∴AO=1


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
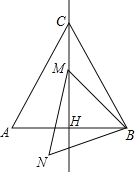
【题目】如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某灯饰商店销售一种进价为每件20元的护眼灯.销售过程中发现,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系可近似地看作一次函数
(元)之间的关系可近似地看作一次函数![]() .物价部门规定该品牌的护眼灯售价不能超过36元.
.物价部门规定该品牌的护眼灯售价不能超过36元.
(1)如果该商店想要每月获得2000元的利润,那么销售单价应定为多少元?
(2)设该商店每月获得利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?
(元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是( )
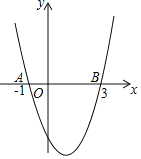
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
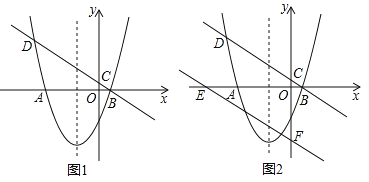
【题目】如图1,抛物线y=ax2+2x+c与x轴交于A(﹣4,0),B(1,0)两点,过点B的直线y=kx+![]() 分别与y轴及抛物线交于点C,D.
分别与y轴及抛物线交于点C,D.
(1)求直线和抛物线的表达式;
(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;
(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
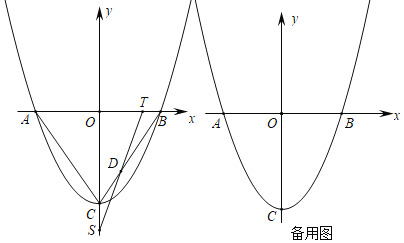
【题目】如图,抛物线y=ax2+bx+c的顶点为C(0,![]() ),与x轴交于A、B两点,且A(﹣1,0).
),与x轴交于A、B两点,且A(﹣1,0).
(1)求抛物线的解析式;
(2)点P从点B出发,以每秒1个单位的速度向点A运动,同时点Q从点C出发,以每秒v个单位的速度向y轴负方向匀速运动,运动时间为t秒,连接PQ交射线BC于点D,当点P到达点A时,点Q停止运动,以点P为圆心,PB为半径的圆与射线BC交于点E.
①求BE的长;当t=1时,求DE的长;
②若在点P,Q运动的过程中,线段DE的长始终是一个定值,求v的值及DE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数![]() 的图象和
的图象和![]() 都在第一象限内,
都在第一象限内,![]() ,
,![]() 轴,且
轴,且![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.

(1)若反比例函数![]() 的图象经过点B,求此反比例函数的解析式;
的图象经过点B,求此反比例函数的解析式;
(2)若将![]() 向下平移
向下平移![]() (m>0)个单位长度,
(m>0)个单位长度,![]() ,
,![]() 两点的对应点同时落在反比例函数图象上,求
两点的对应点同时落在反比例函数图象上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
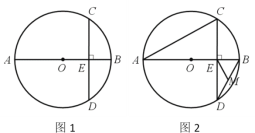
【题目】已知AB是⊙O的直径,C是⊙O上的一点(不与点A,B重合),过点C作AB的垂线交⊙O于点D,垂足为E点.
(1)如图1,当AE=4,BE=2时,求CD的长度;
(2)如图2,连接AC,BD,点M为BD的中点.求证:ME⊥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区![]() 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
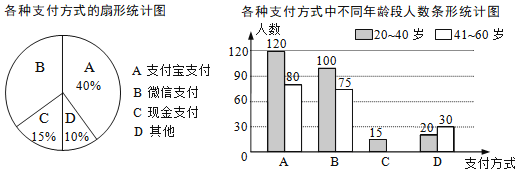
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中![]() 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com