
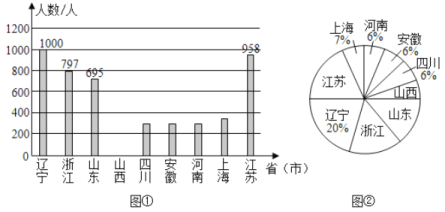
【题目】2020年春节前夕“新型冠状病毒”爆发.疫情就是命令,防控就是使命.全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为_____人;
②请将条形统计图补充完整;
(2)请求出扇形统计图中“山西”所对应扇形的圆心角的度数;
(3)本次山西驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生的概率.
【答案】(1)①5000;②详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)①根据辽宁的人数和所占的百分比求出2月9日当天驰援武汉的医护工作者的总人数;
②先求出江苏、浙江和山东所占的百分比,再用整体1减去各省份所占的百分比,求出山西所占的百分比,再用总人数乘以山西所占的百分比即可补全统计图;
(2)用山西所占的百分比乘以360°即可得出答案;
(3)根据题意画出树状图得出所有等情况数和同时安排王医生和李医生的情况数,然后根据概率公式即可得出答案.
(1)①2月9日当天驰援武汉的医护工作者的总人数为:1000÷20%=5000(人),
②江苏所占的百分比是:![]() ×100%=19.16%;
×100%=19.16%;
浙江所占的百分比是:![]() ×100%=15.94%;
×100%=15.94%;
山东所占的百分比是:![]() ×100%=13.9%;
×100%=13.9%;
则山西所占的百分比是:1-19.16%-7%-6%-6%-6%-13.9%-15.94%-20%=6%,
山西的人数是5000×6%=300(人),补图如下:
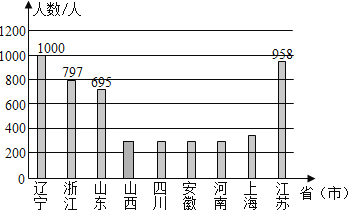
故答案为:5000;
(2)“山西”所对应扇形的圆心角的度数是360°×6%=21.6°;(3)这5名医护工作者分别用1,2,3,4,5表示,其中王医生用1表示,李医生用2表示,根据题意画图如下:
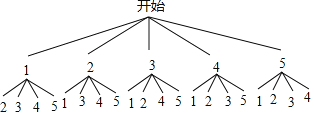
共有20种等情况数,其中同时安排王医生和李医生的有2种,
则同时安排王医生和李医生的概率![]() .
.


科目:初中数学 来源: 题型:
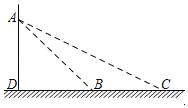
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
查看答案和解析>>
科目:初中数学 来源: 题型:
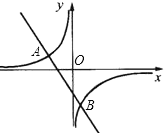
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值>反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
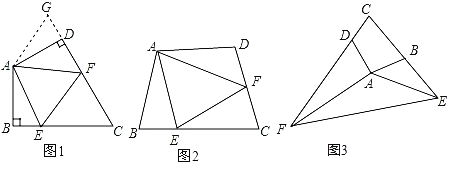
【题目】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠FAD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;
(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
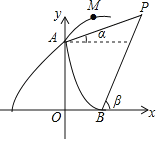
【题目】如图是某导弹发射车在山顶A处进行射击训练的示意图,点A在y轴上,与原点O的距离是8百米(为了计算方便,我们把本题中的距离用百米作单位).此导弹发射车在A处进行某个角度的射击训练,点M是导弹向右上射出后某时刻的位置.忽略空气阻力,实验表明:导弹射出t秒时,点M,A的水平距离是vt百米,点M与x轴(水平)的竖直距离是(8+vt﹣5t2)百米(v的值由发射者设定).在点A和x轴上的点B处观测射击目标P的仰角分别是a和β,OB=3百米,tanα=![]() .tanβ=
.tanβ=![]() .
.
(1)若v=7,完成下列问题:
①当点M,A的水平距离是7百米时,点M到x轴的距离是 百米;
②设点M坐标为(x,y),求y与x的关系式(不必写x的取值范围).
(2)按(1)的射击方式,能否命中目标P?请说明理由.
(3)目标以m百米/秒的速度从点P向右移动,当v![]() 时,若能使目标被击中,求m的取值范围.
时,若能使目标被击中,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,点
,点![]() 为抛物线对称轴上一动点.
为抛物线对称轴上一动点.
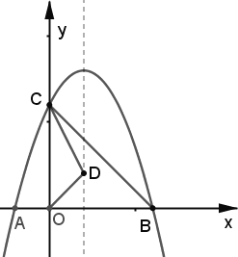
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)连接![]() ,求
,求![]() 周长的最小值;
周长的最小值;
(3)在抛物线上是否存在一点![]() .使以
.使以![]() 为顶点的四边形是以
为顶点的四边形是以![]() 为边的平行四边形?若存在,请直接写出
为边的平行四边形?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD,若AC=10cm,∠BAC=36°,则图中阴影部分的面积为_____.
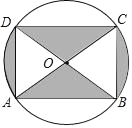
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
⑴如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
⑵如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
⑶当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com