
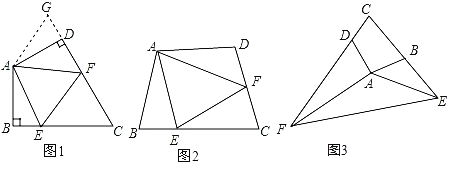
【题目】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠FAD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;
(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.
【答案】(1)∠BAE+∠FAD=∠EAF,理由见解析;(2)仍成立,理由见解析;(3)∠EAF=180°﹣![]() ∠DAB,见解析
∠DAB,见解析
【解析】
(1)延长FD到点G,使DG=BE,连接AG,证明△ADG≌△ABE和△AEF≌△AGF即可得出答案;
(2)延长FD到点G,使DG=BE,连接AG,证明△ADG≌△ABE和△AEF≌△AGF即可得出答案;
(3)在DC延长线上取一点G,使得DG=BE,连接AG,证明△ADG≌△ABE和△AEF≌△AGF即可得出答案.
解:(1)∠BAE+∠FAD=∠EAF.理由:
如图1,延长FD到点G,使DG=BE,连接AG,
∵AB=AD,∠B=∠ADG=90°,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AE=AG,
∵EF=BE+FD=DG+FD=GF,AF=AF,
∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.
故答案为:∠BAE+∠FAD=∠EAF;
(2)仍成立,理由:
如图2,延长FD到点G,使DG=BE,连接AG,
∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,
∴∠B=∠ADG,
又∵AB=AD,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AE=AG,
∵EF=BE+FD=DG+FD=GF,AF=AF,
∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;
(3)∠EAF=180°﹣![]() ∠DAB.
∠DAB.
证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∴∠ADC=∠ABE,
又∵AB=AD,
∴△ADG≌△ABE(SAS),
∴AG=AE,∠DAG=∠BAE,
∵EF=BE+FD=DG+FD=GF,AF=AF,
∴△AEF≌△AGF(SSS),
∴∠FAE=∠FAG,
∵∠FAE+∠FAG+∠GAE=360°,
∴2∠FAE+(∠GAB+∠BAE)=360°,
∴2∠FAE+(∠GAB+∠DAG)=360°,
即2∠FAE+∠DAB=360°,
∴∠EAF=180°﹣![]() ∠DAB.
∠DAB.




科目:初中数学 来源: 题型:
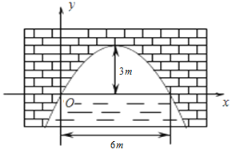
【题目】如图是抛物线形的拱桥,当拱顶离水面3m时,水面宽6m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式;
(2)如果水面上升1m,则水面宽度减少多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A→B→D相交于N,设运动时间为t秒:
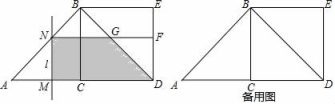
(1)填空:当点M在AC上时,BN= (用含t的代数式表示);
(2)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由;
(3)过点N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
乙小区:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据
成绩x(分) | 60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 |
甲小区 | 2 | 5 | a | b |
乙小区 | 3 | 7 | 5 | 5 |
分析数据
统计量 | 平均数 | 中位数 | 众数 |
甲小区 | 85.75 | 87.5 | c |
乙小区 | 83.5 | d | 80 |
应用数据
(1)填空:a= ,b= ,c= ,d= ;
(2)若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 经过点
经过点![]() ,且垂直于x轴,直线
,且垂直于x轴,直线![]() :
:![]() (
(![]() )经过点
)经过点![]() ,与
,与![]() 交于点
交于点![]() ,
,![]() .点
.点![]() 是线段
是线段![]() 上一点,直线
上一点,直线![]() 轴,交
轴,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点.双曲线
的中点.双曲线![]() (
(![]() )经过点
)经过点![]() ,与
,与![]() 交于点
交于点![]() .
.
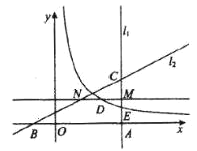
(1)求![]() 的解析式;
的解析式;
(2)当点![]() 是
是![]() 中点时,求点
中点时,求点![]() 的坐标;
的坐标;
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春节前夕“新型冠状病毒”爆发.疫情就是命令,防控就是使命.全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
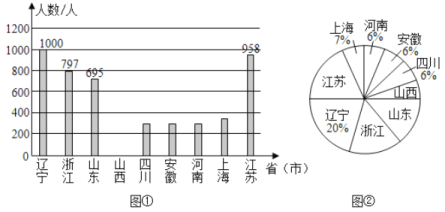
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为_____人;
②请将条形统计图补充完整;
(2)请求出扇形统计图中“山西”所对应扇形的圆心角的度数;
(3)本次山西驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
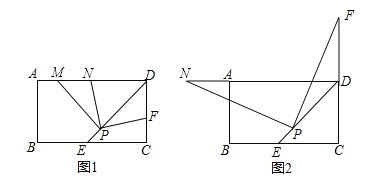
【题目】矩形ABCD中,DE平分∠ADC交BC边于点E,P为DE上的一点(PE<PD),PM⊥PD,PM交AD边于点M.
(1)若点F是边CD上一点,满足PF⊥PN,且点N位于AD边上,如图1所示.
求证:①PN=PF;②DF+DN=![]() DP;
DP;
(2)如图2所示,当点F在CD边的延长线上时,仍然满足PF⊥PN,此时点N位于DA边的延长线上,如图2所示;试问DF,DN,DP有怎样的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形 ABCDEF的中心与坐标原点O重合,其中A(-2,0).将六边形 ABCDEF绕原点O按顺时针方向旋转2018次,每次旋转60°,则旋转后点A的对应点A'的坐标是( ).
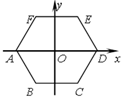
A. (1,![]() ) B. (
) B. (![]() ,1) C. (1,
,1) C. (1,![]() ) D. (-1,
) D. (-1,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com