
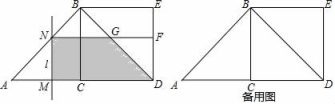
【题目】如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A→B→D相交于N,设运动时间为t秒:
(1)填空:当点M在AC上时,BN= (用含t的代数式表示);
(2)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由;
(3)过点N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值.
【答案】(1)BN=2![]() ﹣
﹣![]() t;(2)当t=4﹣
t;(2)当t=4﹣![]() 或t=3或t=2时,△DNE是等腰三角形;(3)当t=
或t=3或t=2时,△DNE是等腰三角形;(3)当t=![]() 时,S取得最大值
时,S取得最大值![]() .
.
【解析】
(1)由等腰直角三角形的性质知AB=2![]() ,MN=AM=t,AN=
,MN=AM=t,AN=![]() ﹣AM=
﹣AM=![]() ﹣t,据此可得;
﹣t,据此可得;
(2)先得出MN=DM=4﹣t,BP=PN=t﹣2,PE=4﹣t,由勾股定理得出NE=![]() ,再分DN=DE,DN=NE,DE=NE三种情况分别求解可得;
,再分DN=DE,DN=NE,DE=NE三种情况分别求解可得;
(3)分0≤t<2和2≤t≤4两种情况,其中0≤t<2重合部分为直角梯形,2≤t≤4时重合部分为等腰直角三角形,根据面积公式得出面积的函数解析式,再利用二次函数的性质求解可得.
(1)如图1,
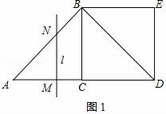
∵∠ACB=90°,AC=BC=2,
∴∠A=∠ABC=45°,AB=2![]() ,
,
∵AM=t,∠AMN=90°,
∴MN=AM=t,AN=![]() AM=
AM=![]() t,
t,
则BN=AB﹣AN=![]()
故答案为:![]()
(2)如图2,
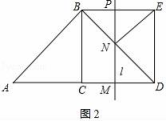
∵AM=t,AC=BC=CD=2,∠BDC=∠DBE=45°,
∴DM=MN=AD﹣AM=4﹣t,
∴DN=![]() DM=
DM=![]() (4﹣t),
(4﹣t),
∵PM=BC=2,
∴PN=2﹣(4﹣t)=t﹣2,
∴BP=t﹣2,
∴PE=BE﹣BP=2﹣(t﹣2)=4﹣t,
则NE=![]() ,
,
∵DE=2,
∴①若DN=DE,则![]() (4﹣t)=2,解得t=4﹣
(4﹣t)=2,解得t=4﹣![]() ;
;
②若DN=NE,则![]() (4﹣t)=
(4﹣t)=![]() ,解得t=3;
,解得t=3;
③若DE=NE,则2=![]() ,解得t=2或t=4(点N与点E重合,舍去);
,解得t=2或t=4(点N与点E重合,舍去);
综上,当t=4﹣![]() 或t=3或t=2时,△DNE是等腰三角形.
或t=3或t=2时,△DNE是等腰三角形.
(3)①当0≤t<2时,如图3,
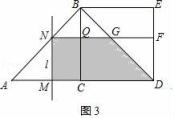
由题意知AM=MN=t,
则CM=NQ=AC﹣AM=2﹣t,
∴DM=CM+CD=4﹣t,
∵∠ABC=∠CBD=45°,∠NQB=∠GQB=90°,
∴NQ=BQ=QG=2﹣t,
则NG=4﹣2t,
∴![]()
当t=![]() 时,S取得最大值
时,S取得最大值![]() ;
;
②当2≤t≤4时,如图4,
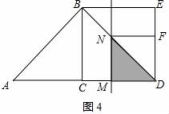
∵AM=t,AD=AC+CD=4,
∴DM=AD﹣AM=4﹣t,
∵∠DMN=90°,∠CDB=45°,
∴MN=DM=4﹣t,
∴S=![]() (4﹣t)2=
(4﹣t)2=![]() (t﹣4)2,
(t﹣4)2,
∵2≤t≤4,
∴当t=2时,S取得最大值2;
综上,当t=![]() 时,S取得最大值
时,S取得最大值![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
【题目】为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
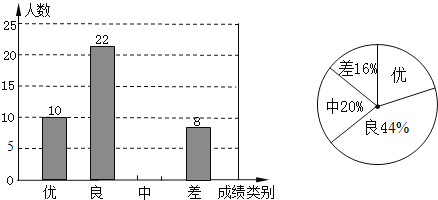
(1)求样本中成绩类别为“中”的人数,并将条形统计图补充完整;
(2)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
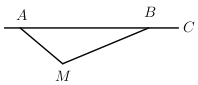
【题目】根据道路管理规定,在广州某段笔直公路上行驶的车辆,限速40千米/时;已知交警测速点![]() 到该公路
到该公路![]() 点的距离为
点的距离为![]() 米,
米,![]() ,
,![]() (如图所示),现有一辆汽车由
(如图所示),现有一辆汽车由![]() 往
往![]() 方向匀速行驶,测得此车从
方向匀速行驶,测得此车从![]() 点行驶到
点行驶到![]() 点所用的时间为2秒.
点所用的时间为2秒.
(1)求测速点![]() 到该公路的距离.
到该公路的距离.
(2)通过计算判断此车是否超速.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、O在数轴上表示的数分别为a、b、c、0,且OA+OB=OC,则下列结论中:其中正确的有( )
①abc>0.
②a(b+c)=0.
③a﹣c=b.
④![]() =﹣1.
=﹣1.
![]()
A.①③④B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
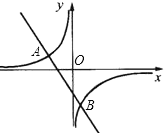
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值>反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
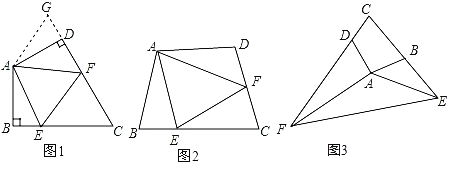
【题目】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF=BE+FD,探究图中∠BAE、∠FAD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;
(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
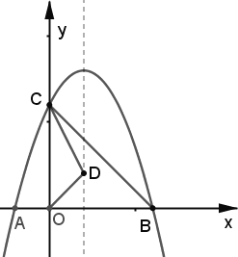
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,点
,点![]() 为抛物线对称轴上一动点.
为抛物线对称轴上一动点.
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)连接![]() ,求
,求![]() 周长的最小值;
周长的最小值;
(3)在抛物线上是否存在一点![]() .使以
.使以![]() 为顶点的四边形是以
为顶点的四边形是以![]() 为边的平行四边形?若存在,请直接写出
为边的平行四边形?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
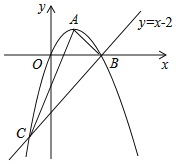
【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线![]() 交于B,C两点.
交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求△ABC的面积;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com