
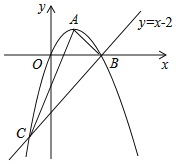
【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线![]() 交于B,C两点.
交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求△ABC的面积;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)y=﹣(x﹣1)2+1,C(﹣1,﹣3);(2)3;(3)存在满足条件的N点,其坐标为(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0)
,0)或(﹣1,0)或(5,0)
【解析】
(1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C点坐标;
(2)设直线AC的解析式为y=kx+b,与x轴交于D,得到y=2x1,求得BD于是得到结论;
(3)设出N点坐标,可表示出M点坐标,从而可表示出MN、ON的长度,当△MON和△ABC相似时,利用三角形相似的性质可得![]() 或
或![]() ,可求得N点的坐标.
,可求得N点的坐标.
(1)∵顶点坐标为(1,1),
∴设抛物线解析式为y=a(x﹣1)2+1,又抛物线过原点,
∴0=a(0﹣1)2+1,解得a=﹣1,∴抛物线解析式为y=﹣(x﹣1)2+1,
即y=﹣x2+2x,联立抛物线和直线解析式可得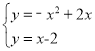 ,
,
解得![]() 或
或![]() ,∴B(2,0),C(﹣1,﹣3);
,∴B(2,0),C(﹣1,﹣3);
(2)设直线AC的解析式为y=kx+b,与x轴交于D,
把A(1,1),C(﹣1,﹣3)的坐标代入得![]() ,
,
解得:![]() ,
,
∴y=2x﹣1,当y=0,即2x﹣1=0,解得:x=![]() ,∴D(
,∴D(![]() ,0),
,0),
∴BD=2﹣![]() =
=![]() ,
,
∴△ABC的面积=S△ABD+S△BCD=![]() ×
×![]() ×1+
×1+![]() ×
×![]() ×3=3;
×3=3;
(3)假设存在满足条件的点N,设N(x,0),则(x,﹣x2+2x),
∴ON=|x|,MN=|﹣x2+2x|,由(2)知,AB=![]() ,BC=3
,BC=3![]() ,
,
∵MN⊥x轴于点N,∴∠ABC=∠MNO=90°,
∴当△ABC和△MNO相似时,有![]() 或
或![]() ,
,
①当![]() 时,∴
时,∴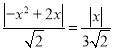 ,即|x||﹣x+2|=
,即|x||﹣x+2|=![]() |x|,
|x|,
∵当x=0时M、O、N不能构成三角形,∴x≠0,∴|﹣x+2|=![]() ,∴﹣x+2=±
,∴﹣x+2=±![]() ,解得x=
,解得x=![]() 或x=
或x=![]() ,此时N点坐标为(
,此时N点坐标为(![]() ,0)或(
,0)或(![]() ,0);
,0);
②当或![]() 时,∴
时,∴ ,即|x||﹣x+2|=3|x|,
,即|x||﹣x+2|=3|x|,
∴|﹣x+2|=3,∴﹣x+2=±3,解得x=5或x=﹣1,
此时N点坐标为(﹣1,0)或(5,0),
综上可知存在满足条件的N点,其坐标为(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0).
,0)或(﹣1,0)或(5,0).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A→B→D相交于N,设运动时间为t秒:
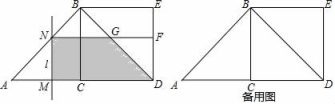
(1)填空:当点M在AC上时,BN= (用含t的代数式表示);
(2)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由;
(3)过点N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,DE平分∠ADC交BC边于点E,P为DE上的一点(PE<PD),PM⊥PD,PM交AD边于点M.
(1)若点F是边CD上一点,满足PF⊥PN,且点N位于AD边上,如图1所示.
求证:①PN=PF;②DF+DN=![]() DP;
DP;
(2)如图2所示,当点F在CD边的延长线上时,仍然满足PF⊥PN,此时点N位于DA边的延长线上,如图2所示;试问DF,DN,DP有怎样的数量关系,并加以证明.
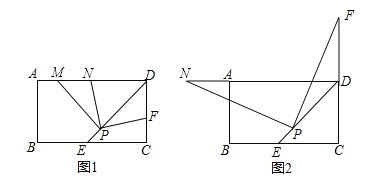
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
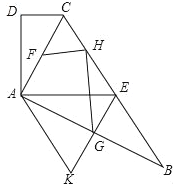
(1)求证:AC2=CD·BC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为线段
为线段![]() 上一点,分别以
上一点,分别以![]() 为底作顶角为
为底作顶角为![]() 的等腰三角形,顶角顶点分别为
的等腰三角形,顶角顶点分别为![]() (点
(点![]() 在
在![]() 的同侧,点
的同侧,点![]() 在
在![]() 的另一侧)
的另一侧)
(1)如图 1,若点![]() 是
是![]() 的中点,则
的中点,则![]()
![]()
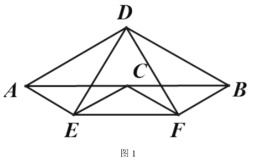
(2)如图 2,若点![]() 不是
不是![]() 的中点,①求证:
的中点,①求证:![]() 为等边三角形;
为等边三角形;

②如图 3,连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
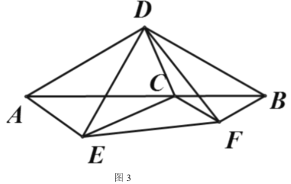
查看答案和解析>>
科目:初中数学 来源: 题型:
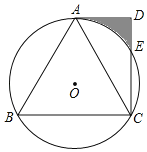
【题目】如图,⊙O为等边△ABC的外接圆,AD∥BC,∠ADC=90°,CD交⊙O于点E.
(1)求证:AD是⊙O的切线;
(2)若DE=2,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
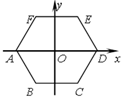
【题目】如图,正六边形 ABCDEF的中心与坐标原点O重合,其中A(-2,0).将六边形 ABCDEF绕原点O按顺时针方向旋转2018次,每次旋转60°,则旋转后点A的对应点A'的坐标是( ).
A. (1,![]() ) B. (
) B. (![]() ,1) C. (1,
,1) C. (1,![]() ) D. (-1,
) D. (-1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ﹔
﹔![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,直线
,直线![]() .
.
(1)当![]() 时,画出直线
时,画出直线![]() 和抛物线
和抛物线![]() ,并直接写出直线
,并直接写出直线![]() 被抛物线
被抛物线![]() 截得的线段长.
截得的线段长.
(2)随着![]() 取值的变化,判断点
取值的变化,判断点![]() 是否都在直线
是否都在直线![]() 上并说明理由.
上并说明理由.
(3)若直线![]() 被抛物线
被抛物线![]() 截得的线段长不小于3,结合函数的图像,直接写出
截得的线段长不小于3,结合函数的图像,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
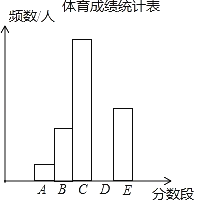
【题目】为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
分数段 | A | B | C | D | E | 合计 |
频数/人 | 12 | 36 | 84 | b | 48 | c |
频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
根据上面的信息,回答下列问题:
(1)统计表中,a= ,b= ,c= ;将频数分布直方图补充完整.
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗? (选填“正确”或“错误”).
(3)若成绩在27分及以上定为优秀,则该市30000名九年级学生中体育成绩为优秀的学生人数约有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com