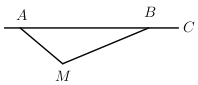
【题目】根据道路管理规定，在广州某段笔直公路上行驶的车辆，限速40千米/时；已知交警测速点
到该公路
点的距离为
米，
，
(如图所示)，现有一辆汽车由往
方向匀速行驶，测得此车从点行驶到点所用的时间为2秒．
（1）求测速点到该公路的距离．
（2）通过计算判断此车是否超速．（参考数据：
，
，
）
名校课堂系列答案科目：初中数学 来源： 题型：
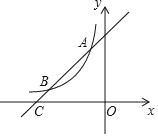
【题目】如图，一次函数y＝x+4的图象与反比例函数y＝
(k为常数且k≠0)的图象交于A(﹣1，a)，B两点，与x轴交于点C．
(1)求a，k的值及点B的坐标；
(2)若点P在x轴上，且S△ACP＝
S△BOC，直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知抛物线
．
（1）抛物线的对称轴为直线________．
（2）当
时，函数值
的取值范围是
，求
和
的值．
（3）当
时，解决下列问题．
①抛物线上一点
到
轴的距离为6，求点的坐标．
②将该抛物线在
间的部分记为
，将在直线
下方的部分沿翻折，其余部分保持不变，得到的新图象记为
，设的最高点、最低点的纵坐标分别为
、
，若
，直接写出
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂有甲种原料69千克，乙种原料52千克，现计划用这两种原料生产A，B两种型号的产品共80件，已知每件A型号产品需要甲种原料0.6千克，乙种原料0.9千克；每件B型号产品需要甲种原料1.1千克，乙种原料0.4千克．请解答下列问题：
（1）该工厂有哪几种生产方案？
（2）在这批产品全部售出的条件下，若1件A型号产品获利35元，1件B型号产品获利25元，（1）中哪种方案获利最大？最大利润是多少？
（3）在（2）的条件下，工厂决定将所有利润的25%全部用于再次购进甲、乙两种原料，要求每种原料至少购进4千克，且购进每种原料的数量均为整数．若甲种原料每千克40元，乙种原料每千克60元，请直接写出购买甲、乙两种原料之和最多的方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE．
（1）求证：△ABE≌△DAF；
（2）若AF=1，四边形ABED的面积为6，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
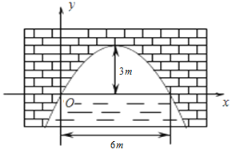
【题目】如图是抛物线形的拱桥，当拱顶离水面3m时，水面宽6m．
(1)建立如图所示的平面直角坐标系，求抛物线的解析式；
(2)如果水面上升1m，则水面宽度减少多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ACB＝90°，AC＝CB＝2，以BC为边向外作正方形BCDE，动点M从A点出发，以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动（M不与A、D重合）；过点M作直线l⊥AD，l与路线A→B→D相交于N，设运动时间为t秒：
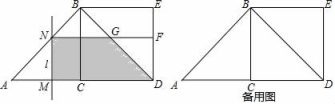
（1）填空：当点M在AC上时，BN＝ （用含t的代数式表示）；
（2）当点M在CD上时（含点C），是否存在点M，使△DEN为等腰三角形？若存在，直接写出t的值；若不存在，请说明理由；
（3）过点N作NF⊥ED，垂足为F，矩形MDFN与△ABD重叠部分的面积为S，求S的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
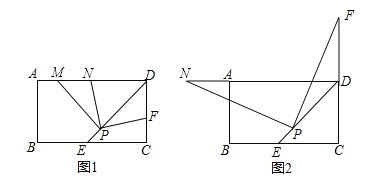
【题目】矩形ABCD中，DE平分∠ADC交BC边于点E，P为DE上的一点（PE＜PD），PM⊥PD，PM交AD边于点M．
（1）若点F是边CD上一点，满足PF⊥PN，且点N位于AD边上，如图1所示．
求证：①PN=PF；②DF+DN=
DP；
（2）如图2所示，当点F在CD边的延长线上时，仍然满足PF⊥PN，此时点N位于DA边的延长线上，如图2所示；试问DF，DN，DP有怎样的数量关系，并加以证明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
