
【题目】在平面直角坐标系中,已知抛物线![]() .
.
(1)抛物线的对称轴为直线________.
(2)当![]() 时,函数值
时,函数值![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 和
和![]() 的值.
的值.
(3)当![]() 时,解决下列问题.
时,解决下列问题.
①抛物线上一点![]() 到
到![]() 轴的距离为6,求点
轴的距离为6,求点![]() 的坐标.
的坐标.
②将该抛物线在![]() 间的部分记为
间的部分记为![]() ,将
,将![]() 在直线
在直线![]() 下方的部分沿
下方的部分沿![]() 翻折,其余部分保持不变,得到的新图象记为
翻折,其余部分保持不变,得到的新图象记为![]() ,设
,设![]() 的最高点、最低点的纵坐标分别为
的最高点、最低点的纵坐标分别为![]() 、
、![]() ,若
,若![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)①
;(3)①![]() 的坐标为
的坐标为![]() 或
或![]() ,②
,②![]() .
.
【解析】
(1)函数的对称轴为:x=![]() ,即可求解;
,即可求解;
(2)函数对称轴为x=1,当-2≤x≤2时,函数值y的取值范围是-4≤y≤b,故y=-4是函数的最小值,即抛物线的顶点为(1,-4),即可求解;
(3)①抛物线上一点P到x轴的距离为6,而顶点坐标为(1,-4),故x2-2x-3=6,即可求解;②分M′在点H下方、上方两种情况分别求解即可.
解:(1)函数的对称轴为:x=![]() ,
,
故答案为:x=1;
(2)函数对称轴为x=1,当-2≤x≤2时,函数值y的取值范围是-4≤y≤b,
故y=-4是函数的最小值,即抛物线的顶点为(1,-4),
把![]() 代入
代入![]() 得
得![]() ,解得
,解得![]()
故抛物线的表达式为:y=x2-2x-3,
则b=(-2)2-2(-2)-3=5;
(3)①∵抛物线上一点P到x轴的距离为6,而顶点坐标为(1,-4),
故x2-2x-3=6,解得:x=1±![]() ,
,
故点P的坐标为(1+![]() ,6)或(1-
,6)或(1-![]() ,6);
,6);
②设图象折叠后顶点M的对应点为M′,点H是x=4函数所处的位置,图象Q为C′M′NH区域,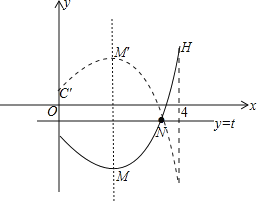
点M(1,-4),点H(4,5),则点M′(1,2t+4),
当点M′在点H下方时,2t+4≤5,t≤![]() ,
,
函数Q的最高点为H,最低点为N,
则5-t≤6,解得:t≥-1,
故-1≤t≤![]() ;
;
当点M′在点H上方时,
同理可得:![]() ≤t≤2;
≤t≤2;
故![]() 的取值范围是:-1≤t≤2.
的取值范围是:-1≤t≤2.


科目:初中数学 来源: 题型:
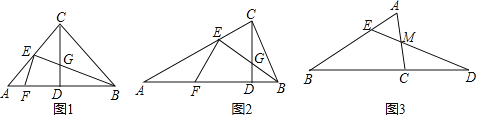
【题目】(1)在△ACB中,∠ACB=90°,CD⊥AB于D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.
①如图1,AC=BC,点E为AC的中点,求证:EF=EG;
②如图2,BE平分∠CBA,AC=2BC,试探究EF与EG的数量关系,并证明你的结论;
(2)如图3,在△ABC中,若![]() ,点E在边AB上,点D在线段BC的延长线上,连接DE交AC于M,∠CMD=60°,DE=2AC,
,点E在边AB上,点D在线段BC的延长线上,连接DE交AC于M,∠CMD=60°,DE=2AC,![]() ,直接写出BE的长.
,直接写出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
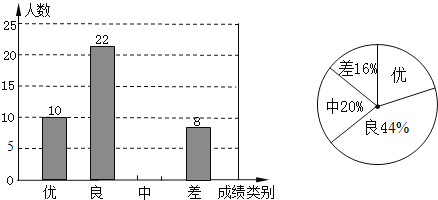
(1)求样本中成绩类别为“中”的人数,并将条形统计图补充完整;
(2)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施,使贫困户的生活条件得到改善,生活质量明显提高。某旗县为了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分四个类别A、非常满意;B、满意;C、基本满意;D、不满意.依据调查数据绘制成条形统计图和扇形统计图(不完整).根据以上信息,解答下列问题:
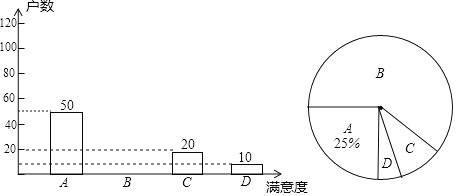
(1)D类别在扇形统计图中对应的圆心角度数是 ;
(2)将条形统计图补充完整;
(3)市扶贫办从该旗县甲乡镇3户和乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
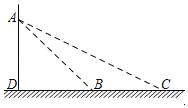
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,某校学生会为了调查学生对雾霾天气知识的了解程度,随机抽取了该校的n名学生做了一次跟踪调查,将调查结果分为四个等级:(A)非常了解.(B)比较了解.(C)基本了解.(D)不了解,并将调查结果绘制成如下两幅不完整统计图.
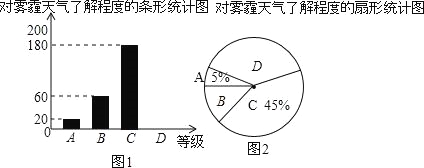
根据统计图提供的信息,解答下列问题:
(1)求n的值;
(2)在调查的n名学生中,对雾霾天气知识不了解的学生有 人,并将条形统计图补充完整.
(3)估计该校1500名学生中,对雾霾天气知识比较了解的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据道路管理规定,在广州某段笔直公路上行驶的车辆,限速40千米/时;已知交警测速点![]() 到该公路
到该公路![]() 点的距离为
点的距离为![]() 米,
米,![]() ,
,![]() (如图所示),现有一辆汽车由
(如图所示),现有一辆汽车由![]() 往
往![]() 方向匀速行驶,测得此车从
方向匀速行驶,测得此车从![]() 点行驶到
点行驶到![]() 点所用的时间为2秒.
点所用的时间为2秒.
(1)求测速点![]() 到该公路的距离.
到该公路的距离.
(2)通过计算判断此车是否超速.(参考数据:![]() ,
,![]() ,
,![]() )
)
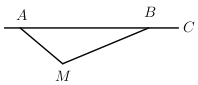
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、O在数轴上表示的数分别为a、b、c、0,且OA+OB=OC,则下列结论中:其中正确的有( )
①abc>0.
②a(b+c)=0.
③a﹣c=b.
④![]() =﹣1.
=﹣1.
![]()
A.①③④B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,点
,点![]() 为抛物线对称轴上一动点.
为抛物线对称轴上一动点.
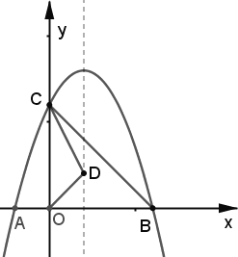
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)连接![]() ,求
,求![]() 周长的最小值;
周长的最小值;
(3)在抛物线上是否存在一点![]() .使以
.使以![]() 为顶点的四边形是以
为顶点的四边形是以![]() 为边的平行四边形?若存在,请直接写出
为边的平行四边形?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com