
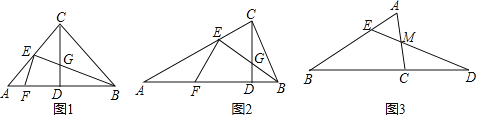
【题目】(1)在△ACB中,∠ACB=90°,CD⊥AB于D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.
①如图1,AC=BC,点E为AC的中点,求证:EF=EG;
②如图2,BE平分∠CBA,AC=2BC,试探究EF与EG的数量关系,并证明你的结论;
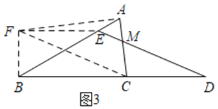
(2)如图3,在△ABC中,若![]() ,点E在边AB上,点D在线段BC的延长线上,连接DE交AC于M,∠CMD=60°,DE=2AC,
,点E在边AB上,点D在线段BC的延长线上,连接DE交AC于M,∠CMD=60°,DE=2AC,![]() ,直接写出BE的长.
,直接写出BE的长.
【答案】(1)①详见解析;②![]() ,理由详见解析;(2)
,理由详见解析;(2)![]() .
.
【解析】
(1)①过E作EM⊥AB于M,EN⊥CD于N,利用等腰直角三角形的性质得到AD=CD,根据三角形中位线的性质证得EN=EM,再证明△EFM≌△EGN即可得到结论;
②作EP⊥AB于点P,EQ⊥CD于点Q,根据BE平分∠ABC,EC⊥BC,EP⊥AB,证得EC=EP,再证明△ECQ∽△ABC,设CQ=a,EQ=2a,根据比例线段求出答案;
(2)过C作CF∥DE,过A作AF⊥AC,交CF于F,连接EF,先证明四边形EFCD是平行四边形,得到∠ABC=∠BEF=30°,即可证得A、F、B、C四点共圆,再利用三角函数求出答案.
(1)①证明:如图1,过E作EM⊥AB于M,EN⊥CD于N,
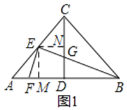
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∴AD=CD,
∵点E为AC的中点,CD⊥AB,EN⊥DC,
![]() ,
,
![]() ,
,
∴EN=EM,
∵∠FEB=90°,∠MEN=90°,
∴∠NEG=∠FEM,
在△EFM和△EGN中,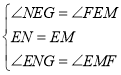 ,
,
∴△EFM≌△EGN(ASA),
∴EF=EG;
②解:![]() ,理由如下:
,理由如下:
如图2,作EP⊥AB于点P,EQ⊥CD于点Q,
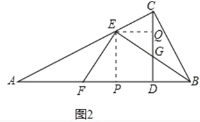
易证:△EFP∽△EGQ,
∴![]() ,
,
∵BE平分∠ABC,EC⊥BC,EP⊥AB,
∴EC=EP,
∵EQ∥AB,
∴∠CEQ=∠A,
∵∠EQC=∠ACB,
∴△ECQ∽△ABC,
∴![]() ,
,
设CQ=a,EQ=2a,则![]() ,
,
∴![]() ,
,
(2)解:如图3,过C作CF∥DE,过A作AF⊥AC,交CF于F,连接EF,
![]() ,
,
∴∠ABC=30°,
∵CF∥DE,
∴∠ACF=∠DMC=60°,
∴∠AFC=30°,
∵∠CAF=90°,
∴CF=2AC,
∵DE=2AC,
∴DE=CF,
∴四边形EFCD是平行四边形,
∴EF∥CD,![]() ,
,
∴∠ABC=∠BEF=30°,
∵∠AFC=∠ABC=30°,
∴A、F、B、C四点共圆,
∴∠FBC+∠CAF=180°,
∴∠FBC=90°,
∵EF∥BC,
∴∠BFE=90°,![]() ,
,
![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:
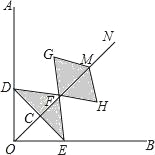
【题目】如图,在由边长为 1 个单位长度的小正方形组成的网格中,建立平面直角坐标系 A(1,7), B(6,3), C(2,3) .
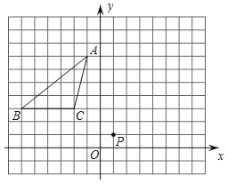
(1)将ABC 绕格点 P(1,1) 顺时针旋转90,得到△ ABC, 画出△ ABC,并写出下列各点坐标: A( , ), B( , ), C( , );
(2)找格点 M ,连CM ,使CM AB ,则点 M 的坐标为( );
(3)找格点 N ,连 BN ,使 BN AC ,则点 N 的坐标为( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
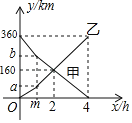
【题目】甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车在相遇之前同时改变了一次速度,并同时到达各自目的地,两车距B地的路程y(km)与出发时间x(h)之间的函数图象如图所示.
(1)分别求甲、乙两车改变速度后y与x之间的函数关系式;
(2)若m=1,分别求甲、乙两车改变速度之前的速度;
(3)如果两车改变速度时两车相距90km,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
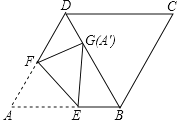
【题目】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要将一份宣传资料进行批量印刷.在甲印刷厂,在收取100元制版费的基础上,每份收费0.5元;在乙印刷厂,在收取40元侧版费的基础上,每份收费0.7元.设该单位要印刷此宣传资料![]() 份(
份(![]() 为正整数).
为正整数).
(Ⅰ)根据题意,填写下表:
印剧数量(份) | 150 | 250 | 350 | 450 | … |
甲印刷厂收费(元) | 175 | ① | 275 | ② | … |
乙印刷厂收费(元) | 145 | 215 | ③ | 355 | … |
(Ⅱ)设在甲印刷厂收费![]() 元,在乙印刷厂收费
元,在乙印刷厂收费![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)当![]() 时,在哪家印刷厂花费少?请说明理由.
时,在哪家印刷厂花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
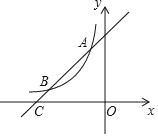
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,直接写出点P的坐标.
S△BOC,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() .
.
(1)抛物线的对称轴为直线________.
(2)当![]() 时,函数值
时,函数值![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 和
和![]() 的值.
的值.
(3)当![]() 时,解决下列问题.
时,解决下列问题.
①抛物线上一点![]() 到
到![]() 轴的距离为6,求点
轴的距离为6,求点![]() 的坐标.
的坐标.
②将该抛物线在![]() 间的部分记为
间的部分记为![]() ,将
,将![]() 在直线
在直线![]() 下方的部分沿
下方的部分沿![]() 翻折,其余部分保持不变,得到的新图象记为
翻折,其余部分保持不变,得到的新图象记为![]() ,设
,设![]() 的最高点、最低点的纵坐标分别为
的最高点、最低点的纵坐标分别为![]() 、
、![]() ,若
,若![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com