
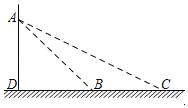
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=mx2﹣4mx+3m(m>0)与x轴的交点为A,B,与y轴的交点为C,D为抛物线的顶点.
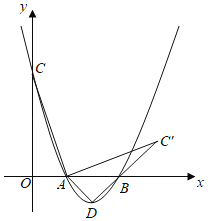
(1)直接写出各点坐标C( , ),D( , );(用m表示)
(2)试说明无论m为何值,抛物线一定经过两个定点并求出这两个定点的坐标;
(3)①将线段AC绕点A顺时针旋转90°得到AC′,求点C′的坐标;
②连接DC',AD,是否存在m,使得△ADC′为等腰三角形?若存在,请求出m;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王、小张和小梅打算各自随机选择本周六的上午或下午去高邮湖的湖上花海去踏青郊游.
(1)小王和小张都在本周六上午去踏青郊游的概率为_______;
(2)求他们三人在同一个半天去踏青郊游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
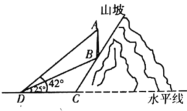
【题目】如图,为加快![]() 网络建设,某移动通信公司在一个坡度为2∶1的山腰上建了一座垂直于水平面的
网络建设,某移动通信公司在一个坡度为2∶1的山腰上建了一座垂直于水平面的![]() 信号通信塔
信号通信塔![]() ,在距山脚
,在距山脚![]() 处水平距离39米的点
处水平距离39米的点![]() 处测得通信塔底
处测得通信塔底![]() 处的仰角是25°,通信塔顶
处的仰角是25°,通信塔顶![]() 处的仰角是42°.请求出通信塔
处的仰角是42°.请求出通信塔![]() 的大约高度(结果保留整数,参考数据:
的大约高度(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
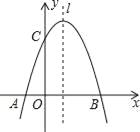
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△DAC=( )

A.1:25B.1:20C.1:18D.1:16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育文化公司为某学校捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.
(1)下列事件是不可能事件的是 .
A.选购乙品牌的D型号 B.既选购甲品牌也选购乙品牌
C.选购甲品牌的A型号和乙品牌的D型号 D.只选购甲品牌的A型号
(2)写出所有的选购方案(用列表法或树状图);
(3)如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com