
【题目】如图,为加快![]() 网络建设,某移动通信公司在一个坡度为2∶1的山腰上建了一座垂直于水平面的
网络建设,某移动通信公司在一个坡度为2∶1的山腰上建了一座垂直于水平面的![]() 信号通信塔
信号通信塔![]() ,在距山脚
,在距山脚![]() 处水平距离39米的点
处水平距离39米的点![]() 处测得通信塔底
处测得通信塔底![]() 处的仰角是25°,通信塔顶
处的仰角是25°,通信塔顶![]() 处的仰角是42°.请求出通信塔
处的仰角是42°.请求出通信塔![]() 的大约高度(结果保留整数,参考数据:
的大约高度(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
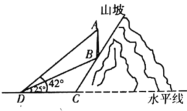
【答案】通信塔AB的大约高度为21米.
【解析】
延长AB交DC延长线于点E,根据坡度的概念设CE=x,得到BE=2x,根据正切的概念列式求出x,得到DE的长,根据正切的定义求出AE,计算即可.
延长AB交DC延长线于点E,则AE⊥DC.
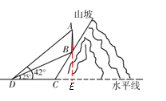
由题意知∠BDC=25°、∠ADE=42°、CD=39米,
∵BC的坡度为2:1
∴设CE=x、则BE=2x、DE=39+x,
在Rt△BDE中,由tan∠BDE=![]() 可得
可得![]() ≈0.5,
≈0.5,
解得:x=13,
∴DE=39+x=52、BE=2x=26,
在Rt△ADE中,AE=DE·tan∠ADE≈52×0.9=46.8,
则AB=AE﹣BE=46.8﹣26=20.8≈21(米),
答:通信塔AB的大约高度为21米.


科目:初中数学 来源: 题型:
【题目】定义:将函数l的图象绕点P(m,0)旋转180°,得到新的函数l'的图象,我们称函数l'是函数关于点P的相关函数.
例如:当m=1时,函数y=(x+1)2+5关于点P(1,0)的相关函数为y=﹣(x﹣3)2﹣5.
(1)当m=0时
①一次函数y=x﹣1关于点P的相关函数为 ;
②点(![]() ,﹣
,﹣![]() )在二次函数y=﹣ax2﹣ax+1(a≠0)关于点P的相关函数的图象上,求a的值.
)在二次函数y=﹣ax2﹣ax+1(a≠0)关于点P的相关函数的图象上,求a的值.
(2)函数y=(x﹣1)2+2关于点P的相关函数y=﹣(x+3)2﹣2,则m= ;
(3)当m﹣1≤x≤m+2时,函数y=x2﹣mx﹣![]() m2关于点P(m,0)的相关函数的最大值为6,求m的值.
m2关于点P(m,0)的相关函数的最大值为6,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=30°,在射线AN上取一点B,使AB=4 cm,过点B作BC⊥AM于点C,点D为边AB上的动点(点D不与点A,点B重合),连接CD,过点D作ED⊥CD交直线AC于点E.在点D由点A到点B运动过程中,设AD=x cm,AE=y cm.
(1)取指定点作图,根据下面表格预填结果,先通过作图确定AD=2 cm时,点E的位置,测量AE的长度.
①根据题意,在答题卡上补全图形;
②把表格补充完整:通过取点、画图、测量,得到了x与y的几组对应值,如表:
x/cm | … |
| 1 |
| 2 |
| 3 |
| … |
y cm | … | 0.4 | 0.8 | 1.0 | m | 1.0 | 0 | 4.0 | … |
则m=______(结果保留一位小数).
(2)在下面的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为______cm.
AD时,AD的长度约为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
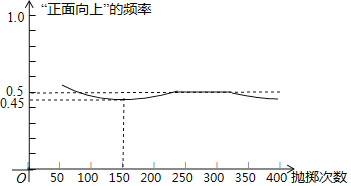
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:连结菱形的一边中点与对边的两端点的线段把它分成三个三角形,如果其中有两个三角形相似,那么称这样的菱形为自相似菱形.
(1)判断下列命题是真命题,还是假命题?
①正方形是自相似菱形;
②有一个内角为60°的菱形是自相似菱形.
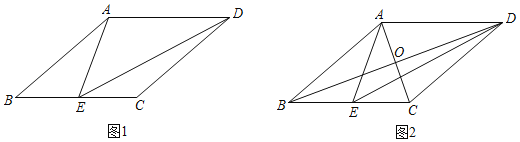
③如图1,若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED.
(2)如图2,菱形ABCD是自相似菱形,∠ABC是锐角,边长为4,E为BC中点.
①求AE,DE的长;
②AC,BD交于点O,求tan∠DBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面图;(要求尺规作图,保留作图痕迹,不写作法)
(2)若这个输水管道有水部分的水面宽AB=32㎝,水最深处的地方高度为8㎝,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
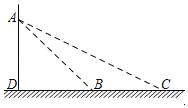
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从共享单车,共享汽车等共享出行到共享充电宝,共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者.小宇和小强分别对共享经济中的“共享出行”和“共享知识”最感兴趣,他们上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为![]() ,
,![]() ,
,![]() ,
,![]() 的四张卡片(除编号和内容外,其余完全相同)他们将这四张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号
的四张卡片(除编号和内容外,其余完全相同)他们将这四张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=4,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=![]() (k>0)的图象经过点D且与边BA交于点E,作直线DE.
(k>0)的图象经过点D且与边BA交于点E,作直线DE.

(1)当点D运动到BC中点时,求k的值;
(2)求![]() 的值;
的值;
(3)连接DA,当△DAE的面积为![]() 时,求k值.
时,求k值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com