
【题目】定义:连结菱形的一边中点与对边的两端点的线段把它分成三个三角形,如果其中有两个三角形相似,那么称这样的菱形为自相似菱形.
(1)判断下列命题是真命题,还是假命题?
①正方形是自相似菱形;
②有一个内角为60°的菱形是自相似菱形.
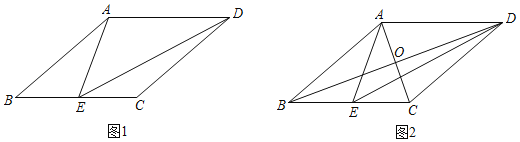
③如图1,若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED.
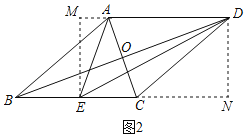
(2)如图2,菱形ABCD是自相似菱形,∠ABC是锐角,边长为4,E为BC中点.
①求AE,DE的长;
②AC,BD交于点O,求tan∠DBC的值.
【答案】(1)见解析;(2)①AE=2![]() ,DE=4
,DE=4![]() ;②tan∠DBC=
;②tan∠DBC=![]() .
.
【解析】
(1)①证明△ABE≌△DCE(SAS),得出△ABE∽△DCE即可;
②连接AC,由自相似菱形的定义即可得出结论;
③由自相似菱形的性质即可得出结论;
(2)①由(1)③得△ABE∽△DEA,得出![]() ,求出AE=2
,求出AE=2![]() ,DE=4
,DE=4![]() 即可;
即可;
②过E作EM⊥AD于M,过D作DN⊥BC于N,则四边形DMEN是矩形,得出DN=EM,DM=EN,∠M=∠N=90°,设AM=x,则EN=DM=x+4,由勾股定理得出方程,解方程求出AM=1,EN=DM=5,由勾股定理得出DN=EM=![]() =
=![]() ,求出BN=7,再由三角函数定义即可得出答案.
,求出BN=7,再由三角函数定义即可得出答案.
解:(1)①正方形是自相似菱形,是真命题;理由如下:
如图3所示:
∵四边形ABCD是正方形,点E是BC的中点,
∴AB=CD,BE=CE,∠ABE=∠DCE=90°,
在△ABE和△DCE中
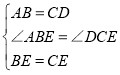 ,
,
∴△ABE≌△DCE(SAS),
∴△ABE∽△DCE,
∴正方形是自相似菱形,
故答案为:真命题;
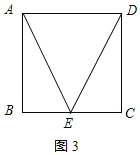
②有一个内角为60°的菱形是自相似菱形,是假命题;理由如下:
如图4所示:
连接AC,
∵四边形ABCD是菱形,
∴AB=BC=CD,AD∥BC,AB∥CD,
∵∠B=60°,
∴△ABC是等边三角形,∠DCE=120°,
∵点E是BC的中点,
∴AE⊥BC,
∴∠AEB=∠DAE=90°,
∴只能△AEB与△DAE相似,
∵AB∥CD,
∴只能∠B=∠AED,
若∠AED=∠B=60°,则∠CED=180°﹣90°﹣60°=30°,
∴∠CDE=180°﹣120°﹣30°=30°,
∴∠CED=∠CDE,
∴CD=CE,不成立,
∴有一个内角为60°的菱形不是自相似菱形,
故答案为:假命题;
③若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,
则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED,是真命题;理由如下:
∵∠ABC=α(0°<α<90°),
∴∠C>90°,且∠ABC+∠C=180°,△ABE与△EDC不能相似,
同理△AED与△EDC也不能相似,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠AEB=∠DAE,
当∠AED=∠B时,△ABE∽△DEA,
∴若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,
则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED,
故答案为:真命题;
(2)①∵菱形ABCD是自相似菱形,∠ABC是锐角,边长为4,E为BC中点,
∴BE=2,AB=AD=4,
由(1)③得:△ABE∽△DEA,
∴![]()
∴AE2=BEAD=2×4=8,
∴AE=2![]() ,DE=
,DE=![]() =
=![]() =4
=4![]() ,
,
故答案为:AE=2![]() ;DE=4
;DE=4![]() ;
;
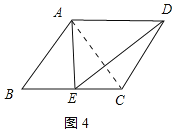
②过E作EM⊥AD于M,过D作DN⊥BC于N,如图2所示:则四边形DMEN是矩形,
∴DN=EM,DM=EN,∠M=∠N=90°,
设AM=x,则EN=DM=x+4,
由勾股定理得:EM2=DE2﹣DM2=AE2﹣AM2,
即(4![]() )2﹣(x+4)2=(2
)2﹣(x+4)2=(2![]() )2﹣x2,
)2﹣x2,
解得:x=1,
∴AM=1,EN=DM=5,
∴DN=EM=![]() =
=![]() ,
,
在Rt△BDN中,
∵BN=BE+EN=2+5=7,
∴tan∠DBC=![]() ,
,
故答案为:![]() .
.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】一张三角形纸片![]() ,其三边之比为
,其三边之比为![]() .小方将纸片对折,第一次使顶点
.小方将纸片对折,第一次使顶点![]() 和
和![]() 重合,第二次使顶点
重合,第二次使顶点![]() 和
和![]() 重合,第三次使顶点
重合,第三次使顶点![]() 和
和![]() 重合,三条折痕依次记为
重合,三条折痕依次记为![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);并求出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
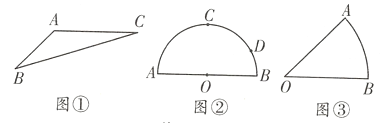
【题目】问题提出
(1)如图①,在![]() 中,
中,![]() ,求
,求![]() 的面积.
的面积.
问题探究
(2)如图②,半圆![]() 的直径
的直径![]() ,
,![]() 是半圆
是半圆![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 是
是![]() 上的动点,试求
上的动点,试求![]() 的最小值.
的最小值.
问题解决
(3)如图③,扇形![]() 的半径为
的半径为![]() 在
在![]() 选点
选点![]() ,在边
,在边![]() 上选点
上选点![]() ,在边
,在边![]() 上选点
上选点![]() ,求
,求![]() 的长度的最小值.
的长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
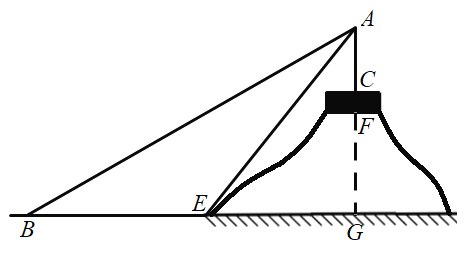
【题目】2018央视中秋晚会在曲阜尼山举行,让全国乃至全世界的目光再一次聚焦曲阜.其中世界最大最高的孔子像,位于晚会场地对面尼山圣境儒宫西侧小山上.来观看晚会的小明想测量一下远处孔子像的高度.如图,小明在B处测得孔子像的顶端A的仰角为![]() ,然后沿着正对孔子像的方向前进了160m到达E处,再次测得孔子像的顶端A的仰角
,然后沿着正对孔子像的方向前进了160m到达E处,再次测得孔子像的顶端A的仰角![]() .已知塑像的底座
.已知塑像的底座![]() ,小山的高度
,小山的高度![]() ,那么孔子像
,那么孔子像![]() 的高度是多少?(参考数据:
的高度是多少?(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
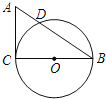
【题目】如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
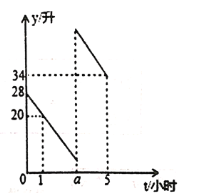
【题目】李师傅驾车从甲地到乙地,途中在加油站加了一次油,加油时,车载电脑显示油箱中剩余油量4升,已知汽车行驶时,每小时耗油量一定,设油箱中剩余油量为![]() (升),汽车行驶时间为
(升),汽车行驶时间为![]() (时),
(时),![]() 与
与![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)求李师傅加油前![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 的值;
的值;
(3)李师傅在加油站的加油量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com