
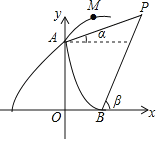
����Ŀ����ͼ��ij�������䳵��ɽ��A���������ѵ����ʾ��ͼ����A��y���ϣ���ԭ��O�ľ�����8���ף�Ϊ�˼��㷽�㣬���ǰѱ����еľ����ð�������λ�����˵������䳵��A������ij���Ƕȵ����ѵ������M�ǵ��������������ijʱ�̵�λ�ã����Կ���������ʵ��������������t��ʱ����M��A��ˮƽ������vt���ף���M��x�ᣨˮƽ������ֱ�����ǣ�8+vt��5t2�����ף�v��ֵ�ɷ������趨�����ڵ�A��x���ϵĵ�B���۲����Ŀ��P�����Ƿֱ���a������OB��3���ף�tan����![]() ��tan����
��tan����![]() ��
��
��1����v��7������������⣺
������M��A��ˮƽ������7����ʱ����M��x��ľ������� �����ף�
�����M����Ϊ��x��y������y��x�Ĺ�ϵʽ������дx��ȡֵ��Χ����
��2������1���������ʽ���ܷ�����Ŀ��P����˵�����ɣ�
��3��Ŀ����m����/����ٶȴӵ�P�����ƶ�����v![]() ʱ������ʹĿ�걻���У���m��ȡֵ��Χ��
ʱ������ʹĿ�걻���У���m��ȡֵ��Χ��
���𰸡���1����10����y����![]() ����2���ܣ����ɼ���������3��0��m��
����2���ܣ����ɼ���������3��0��m��![]() ��
��
��������
��1���ٸ���ˮƽ������7����֪��vt��7����v��7�����t��1���ٴ����M��x�ᣨˮƽ������ֱ�����ǣ�8+vt��5t2�������У��ɵý��ۣ�
�ڸ��ݵ�M����Ϊ��x��y��������֪��M��vt��8+vt��5t2����v��7�����з�����ɵý��ۣ�
��2�������P�����꣬���������ߵĽ���ʽ��������������Ŀ��P��
��3���ɣ�2��֪��7��v��6![]() ����v�����ֵ����M�ĺ��������б�ʾ��y��x�Ĺ�ϵʽ���ɣ�2��֪��P��7��10��������P��������ƽ�ƣ���P�������겻�䣬����10������ɵ�x��ֵ������ʱ�䣬�Ӷ��ý��ۣ�
����v�����ֵ����M�ĺ��������б�ʾ��y��x�Ĺ�ϵʽ���ɣ�2��֪��P��7��10��������P��������ƽ�ƣ���P�������겻�䣬����10������ɵ�x��ֵ������ʱ�䣬�Ӷ��ý��ۣ�
��1���ٵ�v��7ʱ��vt��7��
��7t��7��t��1��
��8+vt��5t2��8+7��1��5��12��15��5��10��
�ʴ�Ϊ��10��
�ڡߵ�M����Ϊ(x��y)��
������ã�M(vt��8+vt��5t2)��v��7����
��![]() ,
,
��t��![]() x��
x��
��y����![]() ��
��
��2���ܣ��������£�
��PC��x���ڵ�C��AD��PC�ڵ�D����ͼ��ʾ��
��OC��AD��a����BC��a��3��
��tan����![]() ��tan����
��tan����![]() ���ã�PD��
���ã�PD��![]() a��PC��
a��PC��![]() ��a��3����
��a��3����
��PC��PD��8����![]() ��a��3����
��a��3����![]() a��8��
a��8��
��ã�a��7����PC��![]() ����7��3����10��
����7��3����10��
���P������Ϊ(7��10)��
��x��7ʱ��y����![]() ��10��
��10��
�������߹���P����������Ŀ��P��
��3��������ã�v��ֵԽ���ڵ��������ԽԶ������Խ����Ŀ�꣬
�ɣ�2��֪��7��v��6![]() ��
��
��v��6![]() ʱ��x��6
ʱ��x��6![]() t��y��8+6
t��y��8+6![]() t��5t2����y����
t��5t2����y����![]() x2+x+8��
x2+x+8��
��Ŀ�������ƶ���y��10������![]() x2+x+8=10��
x2+x+8=10��
��ã�x1��12��x2��![]() ���ᣩ��
���ᣩ��
�൱y��10ʱ���ڵ�������Զ���12���ף���ʱ��![]() ��
��![]() ��
��![]() ���룩��
���룩��
��![]() m��12��7����m��
m��12��7����m��![]() ��
��
��0��m��![]() ��
��


 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
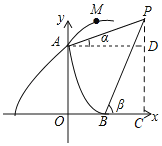
����Ŀ��Ϊ��Ӧ���˿����仯���⣬���Ҵ�����չ������ҵ��ij���ϻ����������ι��ж����������ʹ�ã�ͼ����һ���ͺŵ��ֶ�����ʵ��ͼ��ͼ��Ϊ�����ʾ��ͼ��������ǰ��Ϊ120cm�����ְ뾶Ϊ24cm��CB=CD=24cm��̤��CB��CD��ֱ���ᵵAD��̤��CB��������ɵĽǷֱ�Ϊ15����30������
��1����ᵵAD�ij���
��2����C�����ĸ߶ȣ���sin15��=0.26��cos15��=0.97����ȷ��1cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
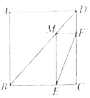
����Ŀ����ͼ���ڱ߳�Ϊ![]() ��������
��������![]() ����
�У���![]() Ϊ�Խ���
Ϊ�Խ���![]() ��һ���㣬
��һ���㣬![]() ��
��![]() ��
��![]() ����
����![]() ����СֵΪ�� ��
����СֵΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɽԺʿ̸����������״��������ʱ˵����������Ҫ���ӷ�������Ҳ���ؿֻţ�������ȥ��Ա�ܼ��ij��������Ŵ����֣�������ע��ͨ�磬��ϴ�֣����˶����ٰ�ҹ����ij����Ϊ�˼�ǿ�������������״����������֪ʶ���˽⣬ͨ����Ⱥ��������״�������ķ���֪ʶ�������������������߲�������2020������״��������ȫ��ͳһ���ԣ�ȫ���������Ծ�����������Ա����Ӽס�������С������ȡ20����Ա�Ĵ���ɼ����������ǵijɼ�����λ���֣�����ͳ�ơ��������������£�
�ռ�����
������85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
������80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
��������
�ɼ�x���֣� | 60��x��70 | 70��x��80 | 80��x��90 | 90��x��100 |
���� | 2 | 5 | a | b |
���� | 3 | 7 | 5 | 5 |
��������
ͳ���� | ƽ���� | ��λ�� | ���� |
���� | 85.75 | 87.5 | c |
���� | 83.5 | d | 80 |
Ӧ������
��1����գ�a���� ����b���� ����c���� ����d���� ����
��2������С������800�˲�����������Ƽ�С���ɼ�����90�ֵ�������
��3����������Ա����ͳ�����ݣ���Ϊ��С��������״����������֪ʶ���ո��ã�����д����������Ա�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ��92��94��96����������m��94��96�����ͨ����ؼ��㲢�Ƚϣ����֣���������ƽ�����ϴ����С����m��ֵ�����ǣ�������
A.91B.92C.95D.98
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020�괺��ǰϦ������״�������������������������ؾ���ʹ����ȫ�����س�Ԯ�人��ҽ�������ߣ�����ҽ�����ĵ�ʹ���뵣����С�ң�Ϊ��ң����Լ���רҵ֪ʶ��Ѫ��֮��������ȫ��Ό������ĸ������ǣ�������2��9�յ���ȫ������ʡ�г�Ԯ�人ҽ�������ߵ�����ͳ��ͼ������������
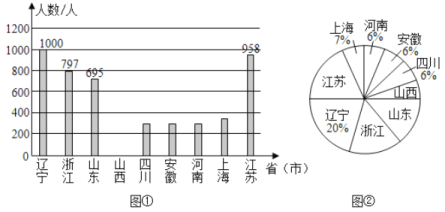
�����������⣺
��1��������ʡ��2��9�յ����Ԯ�人��ҽ�������ߵ�������Ϊ_____�ˣ�
���뽫����ͳ��ͼ����������
��2�����������ͳ��ͼ�С�ɽ��������Ӧ���ε�Բ�ĽǵĶ�����
��3������ɽ����Ԯ�人��ҽ���������У���5�˱���ȥ��֢������ҽ������ҽ���������У����ӱ�����5�����������2�ˣ���ͬʱ������ҽ������ҽ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�༶ѧ����ѧ��ǰԤϰ�ľ��������֣��ʦ�Ա��ಿ��ѧ��������Ϊ��һ���µĸ��ٵ��飬������������Ϊ���ࣺA���ܺã�B���Ϻã�C��һ�㣻D������꣬�������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺

��1��C��Ů������ ������D���������� ����������������ͳ��ͼ����������
��2������ͳ��ͼ������ǰԤϰ���������Ӧ��Բ�ĽǶ������� ����
��3��Ϊ�˹�ͬ������֣��ʦ��ӱ������A���D��ѧ���и��������ȡһλͬѧ������һ��һ������ѧϰ�����û���״ͼ���б��ķ��������ѡ��λͬѧǡ����һ��һŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC��10���ף�BC��12���ף�D��BC���е㣬��P��B��������a����/�루a��0�����ٶ���BA�������A�˶�����Qͬʱ��1����/����ٶȴ�D��������DB�������B�˶�������һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶��������ǵ��˶�ʱ��Ϊt��.
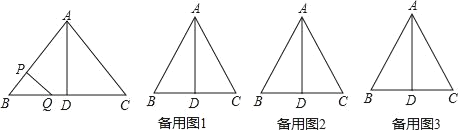
��1����a��2����ôtΪ��ֵʱ��BPQ���BDA���ƣ�
��2����֪MΪAC��һ�㣬����t��![]() ʱ���ı���PQCM��ƽ���ı��Σ�����ʱ��P���˶��ٶ�.
ʱ���ı���PQCM��ƽ���ı��Σ�����ʱ��P���˶��ٶ�.
��3����P��Q�����˶������У�Ҫʹ�߶�PQ��ijһʱ��ƽ�֡�ABD���������P���˶��ٶ�Ӧ������ʲô��Χ�ڣ�����ʾ������һԪ���η��̣������µĽ��ۣ���x1x2�Ƿ���ax2+bx+c��0��a��0��������������x1+x2����![]() ��x1x2��
��x1x2��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���B��60����AB��2��MΪ��AB���е㣬NΪ��BC��һ���㣨�����B�غϣ�������BMN��ֱ��MN�۵���ʹ��B���ڵ�E��������DE��CE������CDEΪ����������ʱ��BN�ij�Ϊ_____��
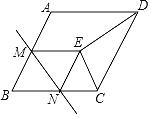
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com