
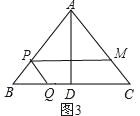
【题目】如图,△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,设它们的运动时间为t秒.
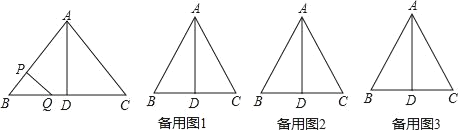
(1)若a=2,那么t为何值时△BPQ与△BDA相似?
(2)已知M为AC上一点,若当t=![]() 时,四边形PQCM是平行四边形,求这时点P的运动速度.
时,四边形PQCM是平行四边形,求这时点P的运动速度.
(3)在P、Q两点运动过程中,要使线段PQ在某一时刻平分△ABD的面积,点P的运动速度应限制在什么范围内?(提示:对于一元二次方程,有如下的结论:若x1x2是方程ax2+bx+c=0(a≠0)的两个根,则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() )
)
【答案】(1)当a=2时,t=![]() 秒或
秒或![]() 秒时,△BPQ与△BDA相似;(2)点P的速度是2.5厘米/秒;(3)点P的速度应大于或等于
秒时,△BPQ与△BDA相似;(2)点P的速度是2.5厘米/秒;(3)点P的速度应大于或等于![]() 厘米/秒.
厘米/秒.
【解析】
(1)根据相似的性质,分情况讨论当△BPQ∽△BDA时及当△BQP∽△BDA时,进行列式计算即可得解;
(2)根据△BPQ∽△BAC,由相似比即可求出P的速度;
(3)根据△BEP∽△BDA,进而求出![]() 和
和![]() 的面积表达式后即可得解.
的面积表达式后即可得解.
(1)当a=2时,BP=2t,DQ=1×t=t,
∵D是BC中点,BC=12,
∴BD=DC=6,
∴![]() ;
;
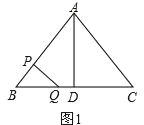
①当△BPQ∽△BDA时,如图1,
则有![]() ,
,
∵BP=2t,BD=6,![]() ,BA=10,
,BA=10,
∴![]() ,
,
解得:![]() ;
;
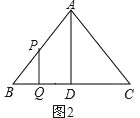
②当△BQP∽△BDA时,如图2,
则有![]() ,
,
∵BP=2t,BD=6,![]() ,BA=10,
,BA=10,
∴![]() ,
,
解得:![]() ;
;
∴当a=2时,![]() 秒或
秒或![]() 秒时,△BPQ与△BDA相似;
秒时,△BPQ与△BDA相似;
(2)当t=![]() 且四边形PQCM是平行四边形时,如图3,
且四边形PQCM是平行四边形时,如图3,
则有PQ∥AC,BP=![]() a,DQ=1×
a,DQ=1×![]() =
=![]() ,BQ=
,BQ=![]() ,
,
∵PQ∥AC,
∴△BPQ∽△BAC,
∴![]() ,
,
∵BP=![]() a,BA=10,BQ=
a,BA=10,BQ=![]() ,BC=12,
,BC=12,
∴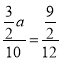 ,
,
解得:a=2.5,
∴点P的速度是2.5厘米/秒;
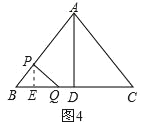
(3)作PE⊥BC,垂足为E,如图4,
∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∵AB=10,BD=6,
∴AD=8,
∵PE⊥BC,AD⊥BC,
∴△BEP∽△BDA,
∴![]() ,
,
∵AD=8,BP=at,BA=10,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵线段PQ平分△ABD的面积,
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
由题可得:![]() ,
,
解得:![]() ,
,
此时![]() ,
,
∴方程![]() 有两个小于6的正实根,
有两个小于6的正实根,
∴点P的速度应大于或等于![]() 厘米/秒.
厘米/秒.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
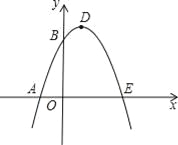
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
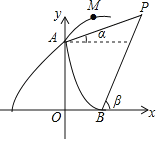
【题目】如图是某导弹发射车在山顶A处进行射击训练的示意图,点A在y轴上,与原点O的距离是8百米(为了计算方便,我们把本题中的距离用百米作单位).此导弹发射车在A处进行某个角度的射击训练,点M是导弹向右上射出后某时刻的位置.忽略空气阻力,实验表明:导弹射出t秒时,点M,A的水平距离是vt百米,点M与x轴(水平)的竖直距离是(8+vt﹣5t2)百米(v的值由发射者设定).在点A和x轴上的点B处观测射击目标P的仰角分别是a和β,OB=3百米,tanα=![]() .tanβ=
.tanβ=![]() .
.
(1)若v=7,完成下列问题:
①当点M,A的水平距离是7百米时,点M到x轴的距离是 百米;
②设点M坐标为(x,y),求y与x的关系式(不必写x的取值范围).
(2)按(1)的射击方式,能否命中目标P?请说明理由.
(3)目标以m百米/秒的速度从点P向右移动,当v![]() 时,若能使目标被击中,求m的取值范围.
时,若能使目标被击中,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
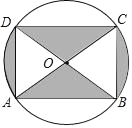
【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD,若AC=10cm,∠BAC=36°,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
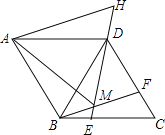
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
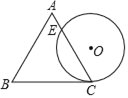
【题目】如图是某商品标牌的示意图,⊙O与等边△ABC的边BC相切于点C,且⊙O的直径与△ABC的高相等,已知等边△ABC边长为4,设⊙O与AC相交于点E,则AE的长为( )
A.![]() B.1C.
B.1C.![]() ﹣1D.
﹣1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解七年级学生最喜欢的学科,从七年级学生中随机抽取部分学生进行“我最喜欢的学科(语文、数学、外语)”试卷调查,请根据两幅统计图中的信息回答下列问题:
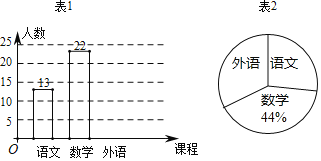
(1)本次抽样调查共抽取了 名学生;最喜欢“外语”的学生有 人;
(2)如果该学校七年级有500人,那么最喜欢外语学科的人数大概有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
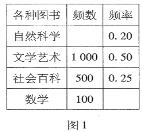
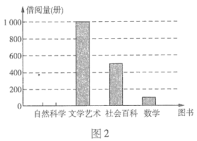
【题目】某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,图1和图2是图书管理员通过采集数据后绘制的两幅不完整的频率分布表与频数分布条形图.请你根据图表中提供的信息,解答以下问题:
(1)填充图1频率分布表中的空格;
(2)在图2中,将表示“自然科学”的部分补充完整;
(3)若该学校打算采购一万册图书,请你估算“数学”类图书应采购多少册较合适?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com