
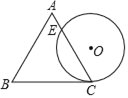
【题目】如图是某商品标牌的示意图,⊙O与等边△ABC的边BC相切于点C,且⊙O的直径与△ABC的高相等,已知等边△ABC边长为4,设⊙O与AC相交于点E,则AE的长为( )
A.![]() B.1C.
B.1C.![]() ﹣1D.
﹣1D.![]()
【答案】B
【解析】
通过求解CE的长度来求出AE的长,连接OC,并过点O作OF⊥CE于F,求出等边三角形的高即可得出⊙O的直径,进而得到半径OC的长度;根据切线和等边三角形的性质不难的得出∠OCF=30°,再在Rt△OFC中,利用特殊角的三角函数值求出FC的长,最后利用垂径定理即可得出CE的长.
连接OC,并过点O作OF⊥CE于F.
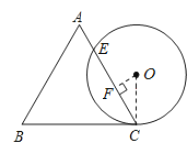
∵△ABC为等边三角形,边长为4,
∴∠ACB=60°,△ABC的高为2![]() .
.
∵等边三角形ABC的高与⊙O的直径相等,
∴⊙O的半径OC=![]() .
.
∵⊙O与BC相切于点C,
∴∠OCB=90°.
∵∠ACB=60°,
∴∠OCF=30°.
∵在Rt△OFC中,∠OCF=30°,OC=![]() ,
,
∴FC=![]() ,
,
∴CE=2FC=3(cm)
∴AE=AC-CE=4-3=1(cm)
故选B.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点.
(1)求直线AD及抛物线的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P,Q,D,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:

请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连接AC,过点D作DE⊥AC,垂足为 E.
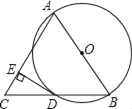
(1)求证:DC=BD;
(2)求证:DE为⊙O的切线;
(3)若AB=12,AD=6![]() ,连接OD,求扇形BOD的面积.
,连接OD,求扇形BOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
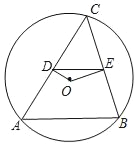
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某小区入口实景图,图2是该入口抽象成的平面示意图,已知入口BC宽3.9米,门卫室外墙上的O点处装有一盏灯,点O与地面BC的距离为3.3米,灯臂OM长1.2米,(灯罩长度忽略不计),∠AOM=60°.

(1)求点M到地面的距离,
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车能否从该入口安全通过?如果能安全通过,请直接写出货车离门卫室外墙AB的最小距离(精确到0.01米);如果不能安全通过,请说明理由.(参考数据:![]() 1.73)
1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
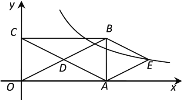
(1)求证:四边形AEBD是菱形;
(2)如果OA=4,OC=2,求出经过点E的反比例函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
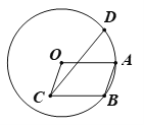
【题目】如图,点A、B在半径为3的⊙O上,以OA、AB为邻边作平行四边形OCBA,作点B关于OA的对称点D,连接CD,则CD的最大值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于 x 的一元二次方程 x2-2(a -1)x a2+ 2=0有两个不相等的实数根.
(1)求实数a的取值范围;
(2)-1可能是方程的一个根吗?若是请求出它的另一个根,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com