
【题目】如图1是某小区入口实景图,图2是该入口抽象成的平面示意图,已知入口BC宽3.9米,门卫室外墙上的O点处装有一盏灯,点O与地面BC的距离为3.3米,灯臂OM长1.2米,(灯罩长度忽略不计),∠AOM=60°.

(1)求点M到地面的距离,
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车能否从该入口安全通过?如果能安全通过,请直接写出货车离门卫室外墙AB的最小距离(精确到0.01米);如果不能安全通过,请说明理由.(参考数据:![]() 1.73)
1.73)
【答案】(1)3.9米;(2)能,0.35米
【解析】
(1)可以过点M作MN⊥OA于点N,根据OM长1.2米,∠AOM=60°.得到ON=0.6米,进而可求得点M到地面的距离;
(2)过点A作AE⊥BA,垂足为A,设货车高AB=3.5米,进而求出AE的长即可说明.
如图所示,
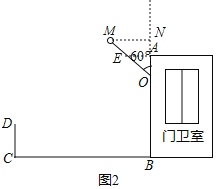
(1)过点M作MN⊥OA于点N,
∵OM长1.2米,∠AOM=60°.
∴ON=0.6米,
∴BN=OB+ON=3.3+0.6=3.9米.
答:点M到地面的距离为3.9米.
(2)一辆总宽2.55米,总高3.5米的货车能从该入口安全通过,理由如下:
过点A作AE⊥BA,垂足为A,
∵该货车高AB=3.5米,
则OA=3.5﹣3.3=0.2
∴AE=OAtan60°=0.2![]() ≈0.35(米)
≈0.35(米)
答:货车离门卫室外墙AB的最小距离为0.35米.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且![]() ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
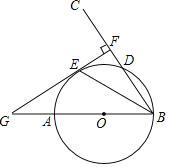
(1)证明:GF是⊙O的切线;
(2)若AG=6,GE=6![]() ,求△GOE的面积.
,求△GOE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
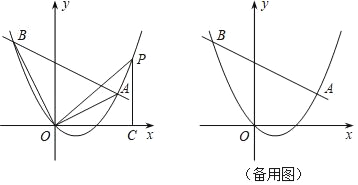
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月24日,华为发布旗下最新款折叠屏手机MateX,如图是这款手机的示意图,当两块折叠屏的夹角为30°时(即∠ABC=30°),测得AC之间的距离为40mm,此时∠CAB=45°.求这款手机完全折叠后的宽度AB长是多少?(结果保留整数,参考数据:![]() )
)
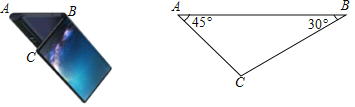
查看答案和解析>>
科目:初中数学 来源: 题型:
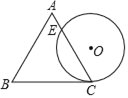
【题目】如图是某商品标牌的示意图,⊙O与等边△ABC的边BC相切于点C,且⊙O的直径与△ABC的高相等,已知等边△ABC边长为4,设⊙O与AC相交于点E,则AE的长为( )
A.![]() B.1C.
B.1C.![]() ﹣1D.
﹣1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
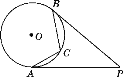
【题目】如图,PA,PB是⊙O的切线,A,B是切点,点C是劣弧AB上的一点,若∠P=40°,则∠ACB等于( )
A. 80° B. 110° C. 120° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
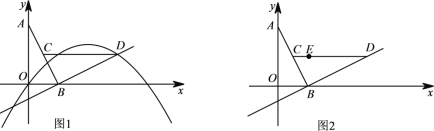
(1)如图1,若该抛物线经过原点O,且a=-![]() .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是3个,请直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动.设运动时间为t秒.
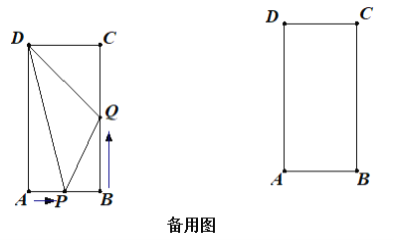
(1)当t=2时,△DPQ的面积为 cm2;
(2)在运动过程中△DPQ的面积能否为26cm2?如果能,求出t的值,若不能,请说明理由;
(3)运动过程中,当 A、P、Q、D四点恰好在同一个圆上时,求t的值;
(4)运动过程中,当以Q为圆心,QP为半径的圆,与矩形ABCD的边共有4个交点时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作思考)画⊙![]() 和⊙
和⊙![]() 的直径
的直径![]() 、弦
、弦![]() ,使
,使![]() ,垂足为
,垂足为![]() (如图1).猜想所画的图中有哪些相等的线段、相等的劣弧?(
(如图1).猜想所画的图中有哪些相等的线段、相等的劣弧?(![]() 除外).
除外).
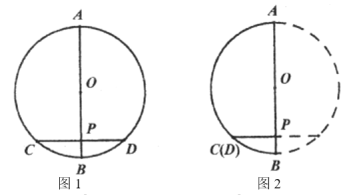
(1)猜想:① ;② ;③ .
操作:将图1中的![]() 沿着直径
沿着直径![]() 翻折,因为圆是轴对称图形,过圆心的任意一条直线都是它的对称轴,所以
翻折,因为圆是轴对称图形,过圆心的任意一条直线都是它的对称轴,所以![]() 与
与![]() 重合,又因为
重合,又因为![]() ,所以射线
,所以射线![]() 与射线
与射线![]() 重合(如图2),于是点
重合(如图2),于是点![]() 与点
与点![]() 重合,从而证实猜想.
重合,从而证实猜想.
(知识应用)图3是某品牌的香水瓶,从正面看上去(如图4),它可以近似看作割去两个弓形后余下的部分与矩形![]() 组合而成的图形(点
组合而成的图形(点![]() 在
在![]() 上),其中
上),其中![]() .
.
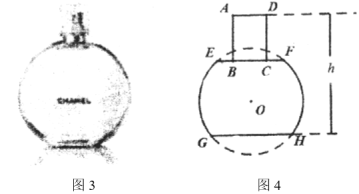
(2)已知⊙![]() 的半径为
的半径为![]() ,
,![]() ,
,![]() ,
,![]() ,求香水瓶的高度
,求香水瓶的高度![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com