
【题目】(操作思考)画⊙![]() 和⊙
和⊙![]() 的直径
的直径![]() 、弦
、弦![]() ,使
,使![]() ,垂足为
,垂足为![]() (如图1).猜想所画的图中有哪些相等的线段、相等的劣弧?(
(如图1).猜想所画的图中有哪些相等的线段、相等的劣弧?(![]() 除外).
除外).
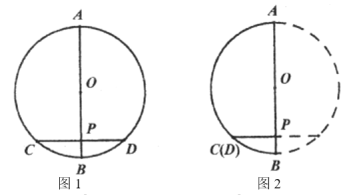
(1)猜想:① ;② ;③ .
操作:将图1中的![]() 沿着直径
沿着直径![]() 翻折,因为圆是轴对称图形,过圆心的任意一条直线都是它的对称轴,所以
翻折,因为圆是轴对称图形,过圆心的任意一条直线都是它的对称轴,所以![]() 与
与![]() 重合,又因为
重合,又因为![]() ,所以射线
,所以射线![]() 与射线
与射线![]() 重合(如图2),于是点
重合(如图2),于是点![]() 与点
与点![]() 重合,从而证实猜想.
重合,从而证实猜想.
(知识应用)图3是某品牌的香水瓶,从正面看上去(如图4),它可以近似看作割去两个弓形后余下的部分与矩形![]() 组合而成的图形(点
组合而成的图形(点![]() 在
在![]() 上),其中
上),其中![]() .
.
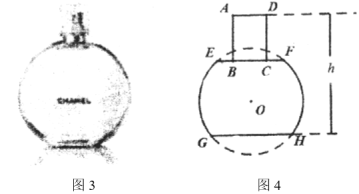
(2)已知⊙![]() 的半径为
的半径为![]() ,
,![]() ,
,![]() ,
,![]() ,求香水瓶的高度
,求香水瓶的高度![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1是某小区入口实景图,图2是该入口抽象成的平面示意图,已知入口BC宽3.9米,门卫室外墙上的O点处装有一盏灯,点O与地面BC的距离为3.3米,灯臂OM长1.2米,(灯罩长度忽略不计),∠AOM=60°.

(1)求点M到地面的距离,
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车能否从该入口安全通过?如果能安全通过,请直接写出货车离门卫室外墙AB的最小距离(精确到0.01米);如果不能安全通过,请说明理由.(参考数据:![]() 1.73)
1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
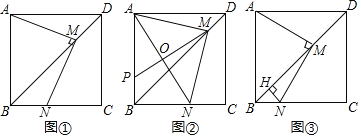
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点
上的一个动点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)如图①,求证:![]() ;
;
(2)如图②,连接![]() 为
为![]() 的中点,
的中点,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 和
和![]() 的长;
的长;
(3)如图③,过点![]() 作
作![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠CAB的角平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=60°,DE=3![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于 x 的一元二次方程 x2-2(a -1)x a2+ 2=0有两个不相等的实数根.
(1)求实数a的取值范围;
(2)-1可能是方程的一个根吗?若是请求出它的另一个根,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.
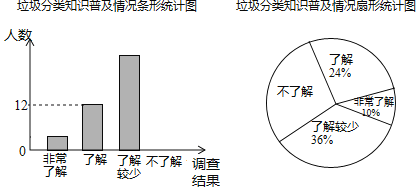
(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边
的边![]() 在正方形
在正方形![]() 的边
的边![]() 上,
上,![]() 是
是![]() 的中点,
的中点,![]() 的平分线
的平分线![]() 过点
过点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,对于下面四个结论:①
,对于下面四个结论:①![]() ;②
;②![]() 且
且![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序号为__________.
,其中正确结论的序号为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
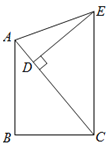
【题目】如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB.分别过点C作CE⊥BC,过点D作DE⊥AC,CE,DE相交于E,连结AE.
(1)求证:△ABC≌△CDE;
(2)若∠AED=20°,求∠ACE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点)及过格点的直线l.
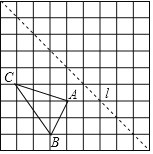
(1)画出△ABC关于直线l对称的△A1B1C1;
(2)将△ABC向上平移3个单位长度,再向左平移1个单位长度,画出平移后的△A2B2C2;
(3)以A、A1、A2为顶点的三角形中,tan∠A2AA1= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com