练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】样本一：92，94，96；样本二：m，94，96．嘉淇通过相关计算并比较，发现：样本二的平均数较大，方差较小．则m的值可能是（　　）

    A.91B.92C.95D.98

    【答案】C

    【解析】

    根据样本二的平均数较大，得出m的值一定大于92，所以从C和D中找，根据方差公式先求出样本一的方差和当m的值是95时样本二的方差，然后根据样本二的平均数较大，方差较小即可得出选项．

    根据样本二的平均数较大，得出m的值一定大于92，所以从C和D中找，

    样本一平均数是：×（92+94+96）＝94，

    方差是：×[（92﹣94）2+（94﹣94）2+（96﹣94）2]＝，

    当m的值是95时，平均数是：×（95+94+96）＝95，

    方差是：×[（95﹣95）2+（94﹣95）2+（96﹣95）2]＝，

    ∵样本二的平均数较大，方差较小，

    ∴C符合条件；

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某超市抽奖规则如下：在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球，它们的形状、大小、质地完全相同，顾客先从盒子里随机取出一个小球，记下小球上标有的数字，然后把小球放回盒子并搅拌均匀，再从盒子中随机取出一个小球，记下小球上标有的数字，并计算两次记下的数字之和若两次所得的数字之和为8，则可获得50元代金券一张：若所得的数字之和为6，则可获得30元代金券一张；若所得的数字之和为5，则可获得15元代金券一张：其他情况都不中奖．

    （1）请用列表或树状图的方法，把抽奖一次可能出现的结果表示出来；

    （2）假如你参加了该超市开业当天的一次抽奖活动，求能中奖的概率P．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

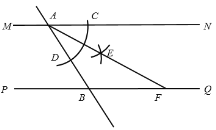
    【题目】如图，直线，直线分别与、相交于点、．小亮同学利用尺规按以下步骤作图：①以点为圆心，以任意长为半径作弧交于点，交于点；②分别以、为圆心，以大于长为半径作弧，两弧在内交于点；③做射线交于点．若，，则的内切圆半径长等于__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为更精准地关爱留守学生，某学校将留守学生的各种情形分成四种类型：A．由父母一方照看；B．由爷爷奶奶照看；C．由叔姨等近亲照看；D．直接寄宿学校．某数学小组随机调查了一个班级，发现该班留守学生数量占全班总人数的20%，并将调查结果制成如下两幅不完整的统计图．

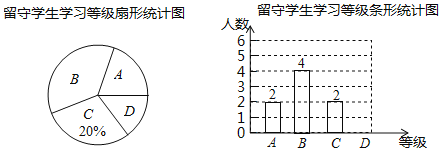
    （1）该班共有　 　名留守学生，B类型留守学生所在扇形的圆心角的度数为　 　；

    （2）将条形统计图补充完整；

    （3）已知该校共有2400名学生，现学校打算对D类型的留守学生进行手拉手关爱活动，请你估计该校将有多少名留守学生在此关爱活动中受益？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与直线相交于，两点，且抛物线经过点

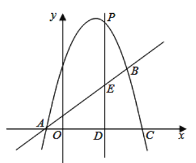
    （1）求抛物线的解析式．

    （2）点是抛物线上的一个动点（不与点点重合），过点作直线轴于点，交直线于点．当时，求点坐标；

    （3）如图所示，设抛物线与轴交于点，在抛物线的第一象限内，是否存在一点，使得四边形的面积最大？若存在，请求出点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，C是线段AB上一点，AC＝5cm，点P从点A出发沿AB以3cm/s的速度向点B运动，点Q从点C出发沿CB以1cm/s的速度向点B运动，两点同时出发，结果点P比点Q先到3s．

    （1）求AB的长；

    （2）设点P，Q出发的时间为ts，求点P没有超过点Q时，t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知x2﹣8x+16﹣m2＝0（m≠0）是关于x的一元二次方程

    （1）证明：此方程总有两个不相等的实数根；

    （2）若等腰△ABC的一边长a＝6，另两边长b、c是该方程的两个实数根，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：△ABC内接于⊙O，连接CO并延长交AB于点E，交⊙O于点D，满足∠BEC＝3∠ACD．

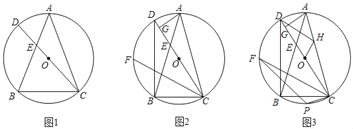
    （1）如图1，求证：AB＝AC；

    （2）如图2，连接BD，点F为弧BD上一点，连接CF，弧CF＝弧BD，过点A作AG⊥CD，垂足为点G，求证：CF+DG＝CG；

    （3）如图3，在（2）的条件下，点H为AC上一点，分别连接DH，OH，OH⊥DH，过点C作CP⊥AC，交⊙O于点P，OH：CP＝1： ，CF＝12，连接PF，求PF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

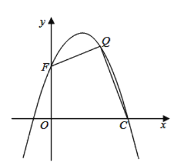
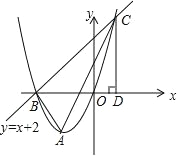
    【题目】如图，已知抛物线 y＝x2+2x 的顶点为 A，直线 y＝x+2 与抛物线交于 B，C 两点．

    （1）求 A，B，C 三点的坐标；

    （2）作 CD⊥x 轴于点 D，求证：△ODC∽△ABC；

    （3）若点 P 为抛物线上的一个动点，过点 P 作 PM⊥x 轴于点 M，则是否还存在除 C 点外的其他位置的点，使以 O，P，M 为顶点的三角形与△ABC 相似？ 若存在，请求出这样的 P 点坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案