
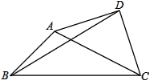
【题目】已知△ABC中,∠ABC=45°,AB=7![]() ,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为___.
,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为___.
【答案】![]()
【解析】
显然直接求BD不好入手,那么就将问题进行转化.注意到△ACD为等腰Rt△,于是以AB为腰向左作等腰Rt△ABE,则易证△ABD与△AEC相似,相似比为![]() ,从而只需求出EC即可,此时∠EBC=135°,于是过E作EF⊥BC于F,则△EFB也为等腰Rt△,算出EF、BF,进而算出EC,问题迎刃而解.
,从而只需求出EC即可,此时∠EBC=135°,于是过E作EF⊥BC于F,则△EFB也为等腰Rt△,算出EF、BF,进而算出EC,问题迎刃而解.
以AB为腰作等腰Rt△ABE,连接EC,
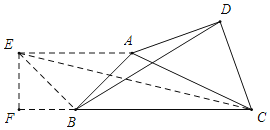
∵△ADC为等腰Rt△,
∴![]() ,∠EAB=∠DAC=45°,
,∠EAB=∠DAC=45°,
∴∠EAB+∠BAC=∠BAC+∠DAC,
∴∠EAC=∠DAB,
∴△EAC∽△BAD,
∴![]() ,
,
作EF⊥BC交BC延长线于F,
∵∠ABC=45°,∠EBA=90°,
∴∠EBF=45°,
∴△EFB为等腰Rt△,
∴EF=FB=![]() EB=
EB=![]() AB=7,
AB=7,
∴EC=![]() =25,
=25,
∴BD=![]() EC=
EC=![]() .
.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
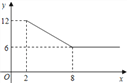
【题目】某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图;B类杨梅深加工后再销售,深加工总费用s(万元)与加工数量t(吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)A类杨梅的销售量为5吨时,它的平均销售价格是每吨多少万元?
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则经营这批杨梅所获得的毛利润(w)为多少万元?(毛利润=销售总收入﹣经营总成本)
(3)若该公司收购20吨杨梅,要使该公司获得30万元毛利润,求直销的A类杨梅有多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=3
,AH=3![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
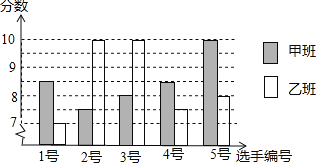
![]() 根据上图填写下表:
根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
| ______ | ______ |
乙班 |
| ______ | 10 |
|
![]() 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
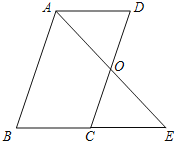
【题目】已知:如图,□ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
![]() 求证:
求证: ![]() ≌
≌![]() ;
;
![]() 连接
连接![]() ,当
,当![]() ______°和
______°和![]() ______°时,四边形ACED是正方形?请说明理由.
______°时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
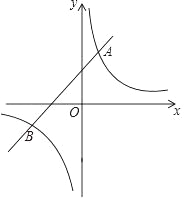
【题目】如图,直线y1=x+2与双曲线y2=![]() 交于A(a,4),B(m,n).
交于A(a,4),B(m,n).
(1)求k值和点B的坐标;
(2)求△AOB的面积;
(3)当y1>y2时请直接写出x的取值范围;
(4)P为x轴上任意一点,当△ABP为直角三角形时,直接写出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=10cm,BC=4cm
(1)图中共有 条线段.
(2)求AD的长.
(3)若点E在线段AB上,且AE=3CE,直接写出BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
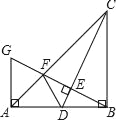
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下三个结论:
①![]() ;
;
②若点D是AB的中点,则AF=![]() AB;
AB;
③若![]() ,则S△ABC=6S△BDF;其中正确的结论的序号是( )
,则S△ABC=6S△BDF;其中正确的结论的序号是( )
A. ①②③ B. ①③ C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图①,数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如,线段AB=0﹣(﹣1)=1:线段:BC=2﹣0=2;线段AC=2﹣(﹣1)=3(大的数减去小的数).
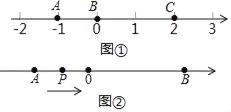
(1)数轴上点A、B表示的数分别是﹣3和2,则AB= ;
(2)数轴上点M表示的数是﹣1,线段MN的长为2,则点N表示的数是 ;
(3)如图②,数轴上点A、B表示的数分别是﹣4和6,动点P从点A出发,沿AB方向以每秒2个单位长度的速度运动,点P运动多少秒时BP=4.并求此时点P表示的数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com