
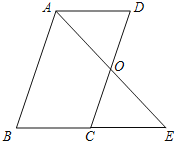
【题目】已知:如图,□ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
![]() 求证:
求证: ![]() ≌
≌![]() ;
;
![]() 连接
连接![]() ,当
,当![]() ______°和
______°和![]() ______°时,四边形ACED是正方形?请说明理由.
______°时,四边形ACED是正方形?请说明理由.
【答案】 45 45
【解析】分析:
(1)由已知条件易得∠D=∠OCE,DO=CO,∠AOD=∠COE,由此即可证得△AOD≌△EOC;
(2)如下图,由△AOD≌△EOC可得AO=EO,DO=BO,从而可得四边形ACED是平行四边形,结合四边形ABCD是平行四边形可得AD=BC=CE,此时要使四边形ACED是正方形,则需∠ACE=90°,AE=CE,故只需∠B=∠AEB=45°即可得到∠BAE=90°,结合BC=CE即可得到所需结论,从而得到四边形ACED是正方形.
详解:
(1)∵点O是CD的中点,
∴DO=CO,
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在![]() 和
和![]() 中
中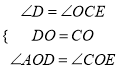 ,
,
∴![]() ≌
≌![]() ;
;
![]() 当
当![]() 和
和![]() 时,四边形ACED是正方形,
时,四边形ACED是正方形,
∵![]() 和
和![]() ,
,
∴![]() ,
,
∵![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形ACED是平行四边形,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴平行四边形ACED是菱形,
∵![]() ,
,
∴![]() ,
,
∴四边形ACED是正方形.
故答案为: ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
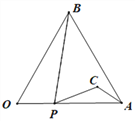
【题目】如图,等边△AOB的边长为4,点P从点O出发,沿OA以每秒1个单位的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.在点P从O向A运动的过程中,当△PCA为直角三角形时t的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都7.5折收费.
(1)若有m名学生,用代数式表示两种优惠方案各需多少元?
(2)当m=70时,采用哪种方案优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
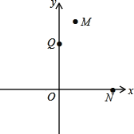
【题目】已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,则点Q的坐标是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
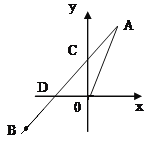
【题目】如图正比例函数y=2x的图像与一次函数 ![]() 的图像交于点A(m,2),一次函数的图象经过点B(-2,-1)与y轴交点为C与x轴交点为D.
的图像交于点A(m,2),一次函数的图象经过点B(-2,-1)与y轴交点为C与x轴交点为D.
(1)求一次函数的解析式;
(2)求![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡度为i=1∶![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点A,D表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=![]() ,连接PB,试探究PA、PB、PC满足的等量关系.
,连接PB,试探究PA、PB、PC满足的等量关系.
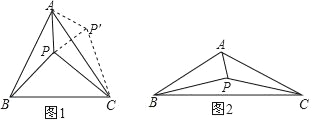
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为 度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为 ;
(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
(3)PA、PB、PC满足的等量关系为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com