
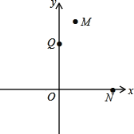
【题目】已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,则点Q的坐标是___.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=3
,AH=3![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
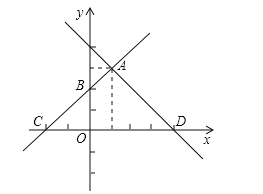
【题目】在如图所示的平面直角坐标系中,直线AB:y=k1x+b1与直线AD:y=k2x+b2相交于点A(1,3),且点B坐标为(0,2),直线AB交x轴负半轴于点C,直线AD交x轴正半轴于点D.
(1)求直线AB的函数解析式;
(2)若△ACD的面积为9,解不等式:k2x+b2>0;
(3)若点M为x轴一动点,当点M在什么位置时,使AM+BM的值最小?求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
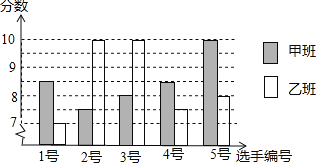
![]() 根据上图填写下表:
根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
| ______ | ______ |
乙班 |
| ______ | 10 |
|
![]() 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
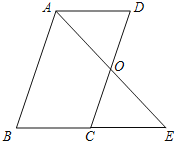
【题目】已知:如图,□ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
![]() 求证:
求证: ![]() ≌
≌![]() ;
;
![]() 连接
连接![]() ,当
,当![]() ______°和
______°和![]() ______°时,四边形ACED是正方形?请说明理由.
______°时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=10cm,BC=4cm
(1)图中共有 条线段.
(2)求AD的长.
(3)若点E在线段AB上,且AE=3CE,直接写出BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)利用求根公式计算,结合①②③你能得出什么猜想?
①方程x2+2x+1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
②方程x2-3x-1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
③方程3x2+4x-7=0的根为x1=_______,x2=________,x1+x2=________,x1·x2=________.
(2)利用求根公式计算:一元二次方程ax2+bx+c=0(a≠0,且b2-4ac≥0)的两根为x1=________,x2=________,x1+x2=________,x1·x2=________.
(3)利用上面的结论解决下面的问题:
设x1、x2是方程2x2+3x-1=0的两个根,根据上面的结论,求下列各式的值:
①![]() ; ②
; ②![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com