
【题目】(1)利用求根公式计算,结合①②③你能得出什么猜想?
①方程x2+2x+1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
②方程x2-3x-1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
③方程3x2+4x-7=0的根为x1=_______,x2=________,x1+x2=________,x1·x2=________.
(2)利用求根公式计算:一元二次方程ax2+bx+c=0(a≠0,且b2-4ac≥0)的两根为x1=________,x2=________,x1+x2=________,x1·x2=________.
(3)利用上面的结论解决下面的问题:
设x1、x2是方程2x2+3x-1=0的两个根,根据上面的结论,求下列各式的值:
①![]() ; ②
; ②![]() .
.
【答案】(1)两根之和等于一次项系数除以二次项系数的相反数,两根之积等于常数项除以二次项系数;① -1;-1;-2;1;② ![]() ;
;![]() ;3;-1;③
;3;-1;③ ![]() ;1;
;1;![]() ;
;![]() ;(2)
;(2) ![]() ;
;![]() ;
;![]() ;
;![]() ;(3)
;(3)![]() ,
,![]() .①3;②
.①3;②![]() .
.
【解析】
(1)利用公式法求解方程的两根,再根据方程的两根可求出![]() ,
,![]() 的值;
的值;
(2)先利用求根公式得出![]() 、
、![]() ,那么就有
,那么就有![]() ,
,![]() ;
;
(5)先利用根与系数的关系求出![]() ,
,![]() 的值,根据
的值,根据![]() ,
,![]() 然后整体代入通分后的式子求值即可.
然后整体代入通分后的式子求值即可.
(1)两根之和等于一次项系数除以二次项系数的相反数,两根之积等于常数项除以二次项系数.
① 由求根公式得:x1=-1,x2=-1,∴x1+x2=-2,x1x2=1;
②由求根公式得:x1=![]() ,x2=
,x2=![]() ,x1+x2=3,x1x2=-1;
,x1+x2=3,x1x2=-1;
③由求根公式得:x1=![]() ,x2=1,∴x1+x2=
,x2=1,∴x1+x2=![]() ,x1x2=
,x1x2=![]() ;
;
故答案为:
① -1;-1;-2;1;
② ![]() ;
;![]() ; 3 ;-1.
; 3 ;-1.
③ ![]() ; 1 ;
; 1 ; ![]() ;
; ![]() .
.
(2)![]() ;
; ![]() ;
;![]() ,
,![]() ;
;
故答案为:![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(3)![]() ,
,![]() .
.
①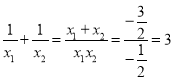 .
.
②![]() .
.


科目:初中数学 来源: 题型:
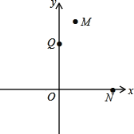
【题目】已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,则点Q的坐标是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点A,D表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )

A. (![]() ,
, ![]() ) B. (
) B. (![]() ,11) C. (2,2
,11) C. (2,2![]() ) D. (
) D. (![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=![]() ,连接PB,试探究PA、PB、PC满足的等量关系.
,连接PB,试探究PA、PB、PC满足的等量关系.
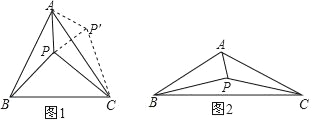
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为 度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为 ;
(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
(3)PA、PB、PC满足的等量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则当x=4时,点R应运动到( )

A. P处B. Q处C. M处D. N处
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com