练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

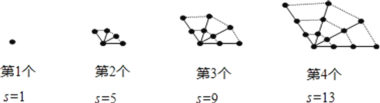
    【题目】观察图中给出的四个点阵，s表示每个点阵中的点的个数，按照图形中的点的个数变化规律，猜想第10个点阵中的点的个数s为（ ）.

    A.B.C.D.

    【答案】D

    【解析】

    观察图形中点的排列规律得到第1个点阵中的点的个数s=1，第2个点阵中的点的个数s=1+4，第3个点阵中的点的个数s=1+4×2=9，第4个点阵中的点的个数s=1+4×3=13，

    …，则第n个点阵中的点的个数s=1+4（n-1），然后把n=10代入计算即可．

    解：∵第1个点阵中的点的个数s=1，

    第2个点阵中的点的个数s=1+4，

    第3个点阵中的点的个数s=1+4×2=9，

    第4个点阵中的点的个数s=1+4×3=13，

    …

    ∴第10个点阵中的点的个数s=1+4×9=37．

    故选择：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．

    （1）求证：△ECF∽△GCE；

    （2）求证：EG是⊙O的切线；

    （3）延长AB交GE的延长线于点M，若tanG=，AH=3，求EM的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，C为线段AB上一点，点D为BC的中点，且AB＝10cm，BC＝4cm

    （1）图中共有　 　条线段．

    （2）求AD的长．

    （3）若点E在线段AB上，且AE＝3CE，直接写出BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

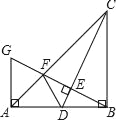
    【题目】如图，在Rt△ABC中，∠ABC=90°，AB=BC，点D是线段AB上的一点，连接CD．过点B作BG⊥CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连接DF，给出以下三个结论：

    ①；

    ②若点D是AB的中点，则AF=AB；

    ③若，则S△ABC=6S△BDF；其中正确的结论的序号是（　　）

    A. ①②③ B. ①③ C. ①② D. ②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）“中国梦”关系每个人的幸福生活，为展现巴中人追梦的风采，我市某中学举行“中国梦我的梦”的演讲比赛，赛后整理参赛学生的成绩，将学的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整，请你根据统计图解答下列问题．

    （1）参加比赛的学生人数共有 名，在扇形统计图中，表示“D等级”的扇形的圆心角为 度，图中m的值为 ；

    （2）补全条形统计图；

    （3）组委会决定从本次比赛中获得A等级的学生中，选出2名去参加市中学生演讲比赛，已知A等级中男生有1名，请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

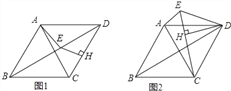
    【题目】已知，在菱形ABCD中，∠ADC=60°，点H为CD上任意一点（不与C、D重合），过点H作CD的垂线，交BD于点E，连接AE．

    （1）如图1，线段EH、CH、AE之间的数量关系是　 　；

    （2）如图2，将△DHE绕点D顺时针旋转，当点E、H、C在一条直线上时，求证：AE+EH=CH．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)利用求根公式计算，结合①②③你能得出什么猜想?

    ①方程x2+2x+1＝0的根为x1＝________，x2＝________，x1+x2＝________，x1·x2＝________．

    ②方程x2-3x-1＝0的根为x1＝________，x2＝________，x1+x2＝________，x1·x2＝________．

    ③方程3x2+4x-7＝0的根为x1＝_______，x2＝________，x1+x2＝________，x1·x2＝________．

    (2)利用求根公式计算：一元二次方程ax2+bx+c＝0(a≠0，且b2-4ac≥0)的两根为x1＝________，x2＝________，x1+x2＝________，x1·x2＝________．

    (3)利用上面的结论解决下面的问题：

    设x1、x2是方程2x2+3x-1＝0的两个根，根据上面的结论，求下列各式的值：

    ①； ②．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：如图①，数轴上线段的长度可以用线段端点表示的数进行减法运算得到，例如，线段AB＝0﹣（﹣1）＝1：线段：BC＝2﹣0＝2；线段AC＝2﹣（﹣1）＝3（大的数减去小的数）．

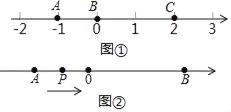
    （1）数轴上点A、B表示的数分别是﹣3和2，则AB＝　 　；

    （2）数轴上点M表示的数是﹣1，线段MN的长为2，则点N表示的数是　 　；

    （3）如图②，数轴上点A、B表示的数分别是﹣4和6，动点P从点A出发，沿AB方向以每秒2个单位长度的速度运动，点P运动多少秒时BP＝4．并求此时点P表示的数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．

    (1)求证：AM=AD+MC．

    (2)若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，试判断AM=AD+MC是否成立？若成立，请给出证明，若不成立，请说明理由；

    查看答案和解析>>

    同步练习册答案