
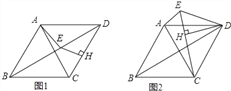
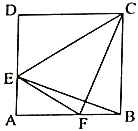
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
【答案】(1) EH2+CH2=AE2;(2)见解析.
【解析】分析:(1)如图1,过E作EM⊥AD于M,由四边形ABCD是菱形,得到AD=CD,∠ADE=∠CDE,通过△DME≌△DHE,根据全等三角形的性质得到EM=EH,DM=DH,等量代换得到AM=CH,根据勾股定理即可得到结论;
(2)如图2,根据菱形的性质得到∠BDC=∠BDA=30°,DA=DC,在CH上截取HG,使HG=EH,推出△DEG是等边三角形,由等边三角形的性质得到∠EDG=60°,推出△DAE≌△DCG,根据全等三角形的性质即可得到结论.
详解:
(1)EH2+CH2=AE2,
如图1,过E作EM⊥AD于M,
∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDE,
∵EH⊥CD,
∴∠DME=∠DHE=90°,
在△DME与△DHE中,
 ,
,
∴△DME≌△DHE,
∴EM=EH,DM=DH,
∴AM=CH,
在Rt△AME中,AE2=AM2+EM2,
∴AE2=EH2+CH2;
故答案为:EH2+CH2=AE2;
(2)如图2,
∵菱形ABCD,∠ADC=60°,
∴∠BDC=∠BDA=30°,DA=DC,
∵EH⊥CD,
∴∠DEH=60°,
在CH上截取HG,使HG=EH,
∵DH⊥EG,∴ED=DG,
又∵∠DEG=60°,
∴△DEG是等边三角形,
∴∠EDG=60°,
∵∠EDG=∠ADC=60°,
∴∠EDG﹣∠ADG=∠ADC﹣∠ADG,
∴∠ADE=∠CDG,
在△DAE与△DCG中,
 ,
,
∴△DAE≌△DCG,
∴AE=GC,
∵CH=CG+GH,
∴CH=AE+EH.




 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
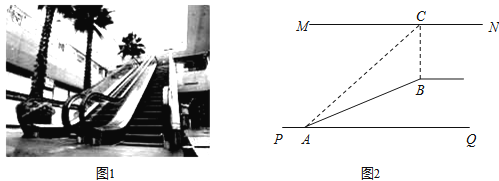
【题目】如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的长度是12.5米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角∠CAQ为45°,坡角∠BAQ为37°,求二楼的层高BC(精确到0.1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为打造“书香校园”,学校每个班级都建立了图书角.七年1班,除了班上每位同学捐出一本书外,三位班委还相约图书城,用班费买些新书.下面是他们的对话内容:

(1)班委A上次买的一套书,图书城的利润是 元,利润率是 .如果当时他买一张会员卡,可省下 元.
(2)当购书的总价(指未打折前的原价)为多少时,办贵宾卡与办会员卡购书一样优惠?
(3)三个班委精心挑选了一批新书,经过计算分析后,发现三种购买方式中,办会员卡购书最省钱,请你直接写出这批书的总价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2.
(2)求点C1在旋转过程中所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个内角为90°,且对角线相等的四边形称为“不完全矩形”.
(1)①如图1,在不完全矩形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,则
,则![]() ____;
____;
②如图2,在平面直角坐标系中,![]() ,
,![]() ,若整点
,若整点![]() 使得四边形
使得四边形![]() 是不完全矩形,则点
是不完全矩形,则点![]() 的坐标是_____;(整点指横坐标、纵坐标都为整数的点)
的坐标是_____;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,在正方形![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,求证:四边形
,求证:四边形![]() 是不完全矩形.
是不完全矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )

A. (![]() ,
, ![]() ) B. (
) B. (![]() ,11) C. (2,2
,11) C. (2,2![]() ) D. (
) D. (![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形OABC中,AB∥OC,∠OAB=90°, ∠OCB=60°,AB=2,OA=2![]() .
.
(1)如图①,连接OB,请直接写出OB的长度;
(2)如图②,过点O作OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,设点P运动的时间为t秒,△OPQ的面积为S(平方单位).
①求S与t之间的函数关系式;
②设PQ与OB交于点M,当△OPM为等腰三角形时,试求出△OPQ的面积S的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com