
【题目】不超过100的自然数中,将凡是3或5的倍数的数相加,其和为__________.
【答案】2418
【解析】
根据题意,设不超过100的自然数中,3的倍数有3、6、9、……、3m,5的倍数有5、10、15、……、5n,(其中m、n为整数),从而求出m和n的值,求出3的所有倍数的和、5的所有倍数的和再减去重复数字的和即可.
解:设不超过100的自然数中,3的倍数最大为3m,5的倍数最大为5n,(其中m、n为整数)
∴3m≤100,5n≤100
解得:m≤![]() ,n≤20
,n≤20
m为33,n为20
∴不超过100的自然数中,3的所有倍数的和为3+6+9+……+3m
=![]()
=![]()
=1683
5的所有倍数的和为5+10+15+……+5n
=![]()
=![]()
=1050
其中既是3的倍数又是5的倍数有15、30、45、60、75、90
∴3的所有倍数和5的所有倍数重复数字的和为15+30+45+60+75+90=315
∴凡是3或5的倍数的数相加,和为1683+1050-315=2418
故答案为:2418.


科目:初中数学 来源: 题型:
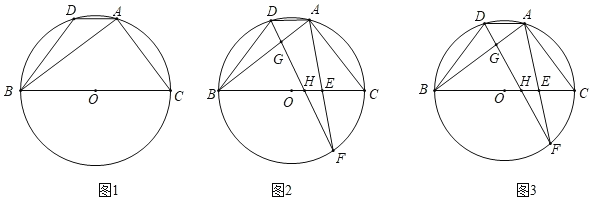
【题目】已知:△ABC内接于⊙O,点D为弧AB上一点,连接AD,BD,且AC=BD.
(1)如图1,求证:AD∥BC;
(2)如图2,点E为BC上一点,连接AE并延长交⊙O于点F,连接DF分别交AB,BC于点G,H,∠BAD+∠CAF=∠BGH,求证:AD=AG;
(3)如图3,在(2)的条件下,当∠BAF=60°,AE=EF,BH=6时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
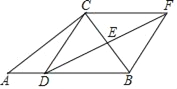
【题目】如图,在△ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)求证:四边形CDBF是平行四边形;
(2)若∠FDB=30°,∠ABC=45°,BC=4![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
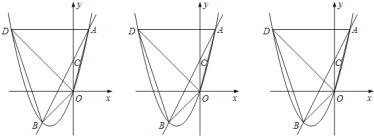
【题目】如图,二次函数y=ax2+bx(a≠0)的图象经过点A(1,4),对称轴是直线x=﹣![]() ,线段AD平行于x轴,交抛物线于点D,在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
,线段AD平行于x轴,交抛物线于点D,在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
(1)求该二次函数的解析式;
(2)设点F是BD的中点,点P是线段DO上的动点,将△BPF沿边PF翻折,得到△B′PF,使△B′PF与△DPF重叠部分的面积是△BDP的面积的![]() ,若点B′在OD上方,求线段PD的长度;
,若点B′在OD上方,求线段PD的长度;
(3)在(2)的条件下,过B′作B′H⊥PF于H,点Q在OD下方的抛物线上,连接AQ与B′H交于点M,点G在线段AM上,使∠HPN+∠DAQ=135°,延长PG交AD于N.若AN+B′M=![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂尔多斯市某百货商场销售某一热销商品A,其进货和销售情况如下:用16000元购进一批该热销商品A,上市后很快销售一空,根据市场需求情况,该商场又用7500元购进第二批该商品,已知第二批所购件数是第一批所购件数的一半,且每件商品的进价比第一批的进价少10元.
(1)求商场第二批商品A的进价;
(2)商场同时销售另一种热销商品B,已知商品B的进价与第二批商品A的进价相同,且最初销售价为165元,每天能卖出125件,经市场销售发现,若售价每上涨1元,其每天销售量就减少5件,问商场该如何定售价,每天才能获得最大利润?并求出每天的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与坐标轴交于
的图像与坐标轴交于![]() 三点,其中点
三点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .动点
.动点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 作匀速运动;同时,动点
作匀速运动;同时,动点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为
作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为![]() 秒.连接
秒.连接![]() .
.
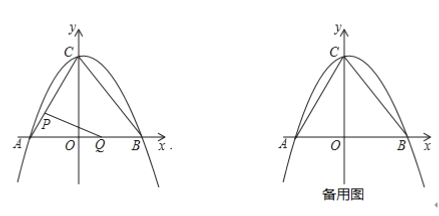
(1)填空:![]() _________,
_________,![]() ________;
________;
(2)在点![]() 运动过程中,
运动过程中,![]() 可能是直角三角形吗?请说明理由;
可能是直角三角形吗?请说明理由;
(3)在![]() 轴下方,该二次函数的图象上是否存在点
轴下方,该二次函数的图象上是否存在点![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形?若存在,请求出运动时间
为直角顶点的等腰直角三角形?若存在,请求出运动时间![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的3月15日是“国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的A商品成本为600元,在标价1000元的基础上打8折销售.
(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?
(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售A商品,其成本、标价与甲卖家一致,以前每周可售出50件,现乙卖家先将标价提高2m%,再大幅降价24m元,使得A商品在3月15日那一天卖出的数量就比原来一周卖出的数量增加了 ![]() m%,这样一天的利润达到了20000元,求m的值.
m%,这样一天的利润达到了20000元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com