
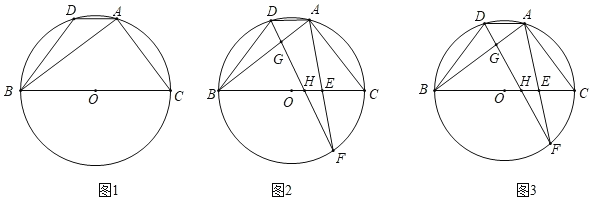
【题目】已知:△ABC内接于⊙O,点D为弧AB上一点,连接AD,BD,且AC=BD.
(1)如图1,求证:AD∥BC;
(2)如图2,点E为BC上一点,连接AE并延长交⊙O于点F,连接DF分别交AB,BC于点G,H,∠BAD+∠CAF=∠BGH,求证:AD=AG;
(3)如图3,在(2)的条件下,当∠BAF=60°,AE=EF,BH=6时,求BE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)7.
【解析】
(1)由AC=BD推出![]() ,进一步推出∠ABC=∠DAB,由平行线的判定即可写出结论; (2)如图2,连接BF,先证∠FBG=∠BGF,再证∠FDA=∠AGD,即可得出结论; (3)如图3,延长BD、FA交于点M,过点B作BN⊥AF于点N,先证AD=AG,AD=AM,BE=EM,再证△FEH∽△FAD,推出AD=2HE,设HE=
,进一步推出∠ABC=∠DAB,由平行线的判定即可写出结论; (2)如图2,连接BF,先证∠FBG=∠BGF,再证∠FDA=∠AGD,即可得出结论; (3)如图3,延长BD、FA交于点M,过点B作BN⊥AF于点N,先证AD=AG,AD=AM,BE=EM,再证△FEH∽△FAD,推出AD=2HE,设HE=![]() ,则AD=
,则AD=![]() ,AG=AM=
,AG=AM=![]() ,BE=BH+HE=
,BE=BH+HE=![]() ,所以BA=BG+GA=
,所以BA=BG+GA=![]() ,EA=EM-AM=
,EA=EM-AM=![]() ,在Rt△ABN中,求出AN=
,在Rt△ABN中,求出AN=![]() AB=
AB=![]() ,BN=
,BN=![]() AN=
AN=![]() ,所以NE=EM-AM-AN=
,所以NE=EM-AM-AN=![]() ,最后在Rt△BNE中,由
,最后在Rt△BNE中,由![]() 可求出
可求出![]() 的值,即可写出BE的长.
的值,即可写出BE的长.
(1)证明:∵AC=BD,∴![]() ,
,
∴∠ABC=∠DAB,∴AD∥BC;
(2)如图2,连接BF,因为![]() ,则∠CAF=∠CBF.
,则∠CAF=∠CBF.

![]() ,
,![]() ∠BAD=∠ABC,
∠BAD=∠ABC,
∴∠BAD+∠CAF=∠CBF+∠ABC=∠FBG.
∵∠BAD+∠CAF=∠BGF,∴∠FBG=∠BGF.
∵∠FBG=∠FDA,∠BGF=∠AGD,
∴∠FDA=∠AGD,∴AD=AG;
(3)如图3,延长BD、FA交于点M,过点B作BN⊥AF于点N.

∵![]() ,∴∠BDF=∠BAF=60°,
,∴∠BDF=∠BAF=60°,
设∠DAG=2α.
∵AD=AG,∴∠ADG=90°﹣α,∠DAM=120°﹣2α,∴∠ADM=30°+α,∴∠DMA=∠ADM=30°+α,∴AD=AM.
∵AD∥BC,∴∠ADM=∠EBD,∴∠EBD=∠DMA,∴BE=EM.
∵![]() ,
,![]() ∠BGH=∠BHG,∴BG=BH=6.
∠BGH=∠BHG,∴BG=BH=6.
∵AD∥BC,∴△FEH∽△FAD,∴![]() .
.
∵AE=EF,∴![]() ,∴
,∴![]() ,∴AD=2HE,
,∴AD=2HE,
设HE=x,则AD=2x,AG=AM=2x,BE=BH+HE=6+x,
∴BA=BG+GA=6+2x,EA=EM﹣AM=6﹣x,
在Rt△ABN中,∠BAN=60°,∠ABN=30°,
∴![]() ,
,![]() ,
,
∴NE=EM﹣AM﹣AN=3﹣2x,
在Rt△BNE中,BN2+NE2=BE2,
即![]() ,
,
解得:![]() (取正值),∴
(取正值),∴![]() .
.


科目:初中数学 来源: 题型:
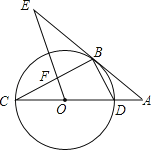
【题目】如图,CD是⊙O的直径,点B在⊙O上,连接BC、BD,直线AB与CD的延长线相交于点A,AB2=ADAC,OE∥BD交直线AB于点E,OE与BC相交于点F.
(1)求证:直线AE是⊙O的切线;
(2)若⊙O的半径为3,cosA=![]() ,求OF的长.
,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
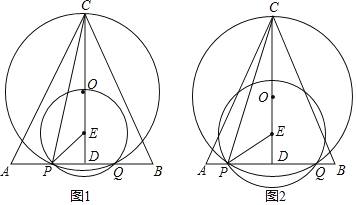
【题目】△ABC中,CA=CB,AB=![]() ,CD⊥AB于点D,CD=5,点O和点E在线段CD上,ED=1,点P在边AB上,以E为圆心,EP为半径的圆与AB边的另一个交点为点Q(点P在点Q的左侧),以O为圆心,OC为半径的圆O恰好经过P、Q两点,联结CP,设线段AP的长度为x.
,CD⊥AB于点D,CD=5,点O和点E在线段CD上,ED=1,点P在边AB上,以E为圆心,EP为半径的圆与AB边的另一个交点为点Q(点P在点Q的左侧),以O为圆心,OC为半径的圆O恰好经过P、Q两点,联结CP,设线段AP的长度为x.
(1)当圆E恰好经过点O时,求圆E的半径;
(2)联结CQ,设∠PCQ的正切值为y,求y与x的函数关系式及定义域;
(3)若∠PED=3∠PCE,求S△PCQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程 7x ![]() (k 13)x k 2 0 ( k 是实数)有两个实数跟 a,b ,且 0 a 1 b 2 ,那么 k 的取值范围是_____.
(k 13)x k 2 0 ( k 是实数)有两个实数跟 a,b ,且 0 a 1 b 2 ,那么 k 的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
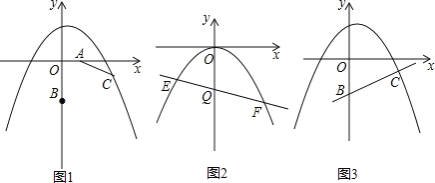
【题目】在如图的直角坐标系中,已知点A(1,0)、B(0,﹣2),将线段AB绕点A按逆时针方向旋转90°至AC,若抛物线y=﹣![]() x2+bx+2经过点C.
x2+bx+2经过点C.
(1)求抛物线的解析式;
(2)如图,将抛物线平移,当顶点至原点时,过Q(0,﹣2)作不平行于x轴的直线交抛物线于E、F两点,问在y轴的正半轴上是否存在一点P,使△PEF的内心在y轴上?若存在,求出点P的坐标;若不存在,说明理由.
(3)在抛物线上是否存在一点M,使得以M为圆心,以![]() 为半径的圆与直线BC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
为半径的圆与直线BC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的4个小球,其中红球3个(记为![]() ,
,![]() ,
,![]() ),黑球1个(记为
),黑球1个(记为![]() ).
).
(1)若先从袋中取出![]() 个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件
个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件![]() ,填空:①若
,填空:①若![]() 为必然事件,则
为必然事件,则![]() 的值为__________;②若
的值为__________;②若![]() 为随机事件,则
为随机事件,则![]() 的取值为_____________;
的取值为_____________;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为![]() 上一点(点P不与点B,C重合),连结AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,
上一点(点P不与点B,C重合),连结AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,![]() 的值始终等于
的值始终等于![]() .则下列说法正确的是( )
.则下列说法正确的是( )
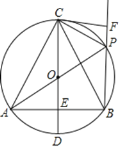
A.①,②都对B.①对,②错C.①错,②对D.①,②都错
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别是边BC、AB的中点,将△BDE绕着点B旋转,点D、E旋转后的对应点分别为点D′、E′,当直线D′E′经过点A时,线段CD′的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com