
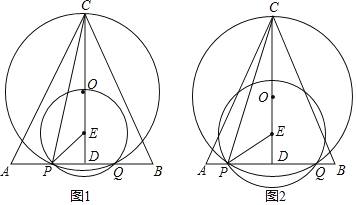
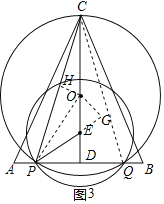
����Ŀ����ABC�У�CA��CB��AB��![]() ��CD��AB�ڵ�D��CD��5����O�͵�E���߶�CD�ϣ�ED��1����P�ڱ�AB�ϣ���EΪԲ�ģ�EPΪ�뾶��Բ��AB�ߵ���һ������Ϊ��Q����P�ڵ�Q����ࣩ����OΪԲ�ģ�OCΪ�뾶��ԲOǡ�þ���P��Q���㣬����CP�����߶�AP�ij���Ϊx��
��CD��AB�ڵ�D��CD��5����O�͵�E���߶�CD�ϣ�ED��1����P�ڱ�AB�ϣ���EΪԲ�ģ�EPΪ�뾶��Բ��AB�ߵ���һ������Ϊ��Q����P�ڵ�Q����ࣩ����OΪԲ�ģ�OCΪ�뾶��ԲOǡ�þ���P��Q���㣬����CP�����߶�AP�ij���Ϊx��
��1����ԲEǡ�þ�����Oʱ����ԲE�İ뾶��
��2������CQ�����PCQ������ֵΪy����y��x�ĺ�����ϵʽ��������
��3������PED��3��PCE����S��PCQ��ֵ��
���𰸡���1��![]() ��5����2��y��
��5����2��y��![]() ��
��![]() ��x��
��x��![]() ������3��
������3��![]()
��������
��1������OP������E�İ뾶Ϊr������OP2��OD2��PE2��DE2�г����̼���������ۣ�
��2������OQ�����ݵȱ߶ԵȽǿɵá�OCQ����OQC��Ȼ��֤����PCQ����DOQ�����ݹ��ɶ��������Ƴ�m��x�Ĺ�ϵ��������������Ǻ����������y��x�ĺ�����ϵʽ��
��3������CQ��OP������O��OH��CP��H����CG��PE��G�����������������ж��ֱ�֤����EPO�ס�ECP����CHO�ס�CDP����OC��OP��m���������������ε������г�����ʽ�������m��ֵ���Ӷ����PQ��CD������������ۣ�
�⣺��1����ͼ1������OP������E�İ뾶Ϊr����PE��OE��r��OP��OC��4��r��OD��r+1��
��CD��AB��
��OP2��OD2��PE2��DE2��
����4��r��2����r+1��2��r2��12��
���![]() ����ȥ����
����ȥ����![]() ��
��
��ԲE�İ뾶r��![]() ��5��
��5��
��2����ͼ2������OQ��
��OQ��OC��
���OCQ����OQC
�ߡ�DOQ����OCQ+��OQC
���DOQ��2��OCQ
�ߡ�PCD����QCD
���PCQ��2��QCD
���PCQ����DOQ
��OC��OQ��m����OD��5��m��
�ɹ��ɶ�����DQ2��m2����5��m��2��10m��25��
����֪��AP��x��
��DQ��![]() ��x��
��x��
��OD��5��m��![]() ��
��![]() ��
��
��y��tan��PCQ��tan��DOQ��![]() ��
��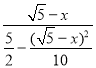 ��
��![]()
��![]()
��![]() ��x��
��x��![]() ��
��
��y��x�ĺ�����ϵʽΪ y��![]() ��
��![]() ��x��
��x��![]() ����
����
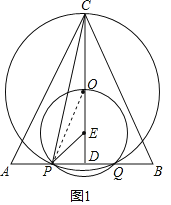
��3����ͼ3������CQ��OP������O��OH��CP��H����CG��PE��G��
��OC��OP��
���PCE����OPC��CH��![]() CP
CP
�ߡ�PED��3��PCE��
���OPE����OPC����PCE��
���EPO�ס�ECP��OH��OG��
��OC��OP��m��
�ߡ�CHO����CDP��90�㣬
���CHO�ס�CDP
��![]() ����
����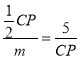
��CP2��10m��CP��![]() ��PD2��10m��25��PE2��10m��24��
��PD2��10m��25��PE2��10m��24��
��![]() ��
��
��![]()
��![]() ��
��
��ã�m1��0����ȥ����![]() ��
��
��PD��![]() ��
��![]() ��PQ��2PD��
��PQ��2PD��![]()
��![]() ��
��![]() ��
��



 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����x2+bx+c��x�Ḻ�����ڵ�A����x���������ڵ�B��4��0������y���������ڵ�C��OC��4OA��S��ABC��24��
��1���������ߵĽ���ʽ��
��2����PΪ��һ������������һ�㣬����P��PD��AB�ڵ�D������AP��y���ڵ�E������E��EG��PD�ڵ�G�����P�ĺ�����Ϊt��t��1����PG�ij���Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£�����B��BF��EG��EG���ӳ����ڵ�F����Q���߶�GF�ϣ�����DQ��PQ������DGQ��DQ�۵���G�ĶԳƵ�Ϊ��H��DH��BF�ڵ�M������MQ���ӳ���DP���ӳ����ڵ�N������DQM��45�㣬tan��PQN��![]() ʱ����ֱ��PQ�Ľ���ʽ��
ʱ����ֱ��PQ�Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
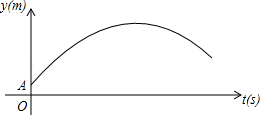
����Ŀ����ͼ��ij�����˶�Ավ�ڵ�O����ϰ���ţ�������������0.5m��A�����������߳�����A��y���ϣ�������ķ��и߶�y����λ��m�������ʱ��t����λ��s��֮�����㺯����ϵy��at2+5t+c����֪�������0.8sʱ�������ĸ߶�Ϊ3.5m��
��1��a���� ����c���� ����
��2����������е�ʱ��Ϊ����ʱ�������������ߣ����߶��Ƕ��٣�
��3����������е�ˮƽ����x����λ��m�������ʱ��t����λ��s��֮����к�����ϵx��10t����֪���ŵĸ߶�Ϊ2.44m��������˶�Ա������������ʱ�������ŵ�ˮƽ����Ϊ28m�����ܷ���ֱ���������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ xOy �У���֪������y= x2 -2px+q��
��1����p=2 ʱ��
�������ߵĶ������������Ϊ____ ___��������Ϊ__________(�ú� q ��ʽ�ӱ�ʾ)��
������ A��-1��y1����B��x2��y2 �������������ϣ���y2 >y1����x2 = m���� m��ȡֵ��Χ��_____________��
��2����֪�� M��3��2�������� M ����ƽ�� 5 ����λ���ȣ��õ��� N����q=6 ʱ�������������߶� MN ǡ��һ�������㣬��Ϻ���ͼ���� p ��ȡֵ��ΧΪ_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����һ�ֽ���Ϊ20Ԫ/���ļ���������������y������������ۼ۸�x��Ԫ/�����ı仯���±���
�۸�x��Ԫ/���� | �� | 30 | 40 | 50 | 60 | �� |
������y������� | �� | 5 | 4 | 3 | 2 | �� |
ͬʱ�����۹����е�������֧���������ۣ��ܼ�40��Ԫ��
��1���۲첢�������е�y��x֮��Ķ�Ӧ��ϵ������ѧ����һ�κ�������������������κ������й�֪ʶд��y���������x��Ԫ/�����ĺ�������ʽ��
��2������ù�˾�������ּ������ľ�������z����Ԫ�������ۼ۸�x��Ԫ/�����ĺ�������ʽ�����ۼ۸�Ϊ����Ԫʱ��������������ֵ�Ƕ��٣�
��3���ù�˾Ҫ�������ܵ���40��Ԫ����д�����ۼ۸�x��Ԫ/������ȡֵ��Χ�������迼�������������ܴ����ۼ۸�Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
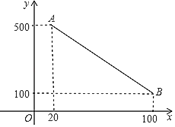
����Ŀ��С��������һ̨���ʽ�Զ�ɨ�ػ���ÿ����ɳ�����ʹ��ʱɨ�ػ����Զ������趨ɨ��ʱ�䣬��ȷ��ɨ�ص��ٶ�(��ʹÿ��ɨ�ؽ���ʱ������������ĵ�������)����ͼ�����趨ɨ��ʱ��������ɨ���ٶ���֮��ĺ���ͼ��(�߶�AB)�������趨ɨ��ʱ��Ϊx���ӣ�ɨ���ٶ�Ϊyƽ������/���ӣ�
(1)��y����x�ĺ�������ʽ��
(2)����С����Ҫɨ�ػ����180ƽ����ɨ��������Ӧ���趨��ɨ��ʱ��Ϊ���ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������һ��������һ���ߵ�2����������һ������30������ô����������ǣ���
A.ֱ��������B.���������C.�۽�������D.ͼ�β���ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�ڽ�����O����DΪ��AB��һ�㣬����AD��BD����AC=BD��
��1����ͼ1����֤��AD��BC��
��2����ͼ2����EΪBC��һ�㣬����AE���ӳ�����O�ڵ�F������DF�ֱ�AB��BC�ڵ�G��H����BAD+��CAF=��BGH����֤��AD=AG��
��3����ͼ3���ڣ�2���������£�����BAF=60�㣬AE=EF��BH=6ʱ����BE�ij���
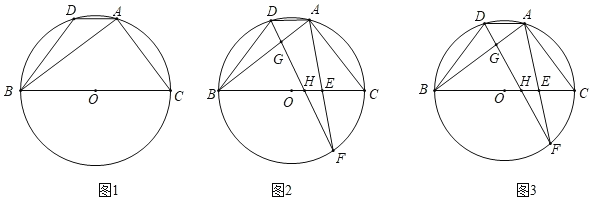
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��AB��������һ�㣬E��BC���е㣬����C��AB��ƽ���ߣ���DE���ӳ����ڵ�F������BF��CD��
��1����֤���ı���CDBF��ƽ���ı��Σ�
��2������FDB=30�㣬��ABC=45�㣬BC=4![]() ����DF�ij���
����DF�ij���
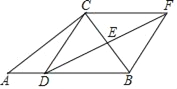
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com