
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c交x轴负半轴于点A,交x轴正半轴于点B(4,0),交y轴正半轴于点C,OC=4OA,S△ABC=24.
(1)求抛物线的解析式;
(2)点P为第一象限抛物线上一点,过点P作PD⊥AB于点D,连接AP交y轴于点E,过点E作EG⊥PD于点G,设点P的横坐标为t(t≤1),PG的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点B作BF⊥EG交EG的延长线于点F,点Q在线段GF上,连接DQ、PQ,将△DGQ沿DQ折叠后,点G的对称点为点H,DH交BF于点M,连接MQ并延长交DP的延长线于点N,当∠DQM=45°,tan∠PQN=![]() 时,求直线PQ的解析式.
时,求直线PQ的解析式.

【答案】(1)y=﹣x2+2x+8;(2)d=﹣t2+4t;(3)y=﹣![]() x+
x+![]() .
.
【解析】
(1)根据所告诉的两个等量关系求出A、C坐标,再将坐标代入解析式即可求出b、c的值.
(2)用t表示相关的竖直线段与水平线段,再根据△PEGPAD列出比例等式化简整理即可得到d与t关系式.
(3)先证明△QFM≌△MHQ.然后作MK⊥QM交DQ于K,过点K作SR⊥FB于R交GD于S,易得△QFM≌△MRK,可以推出R是BF中点,进而得SK=BF=![]() GQ,tan∠N=tan∠QMF=
GQ,tan∠N=tan∠QMF=![]() ,作PT⊥QN于T,结合tan∠PQN=
,作PT⊥QN于T,结合tan∠PQN=![]() 可以导出
可以导出![]() ,得到PG=4﹣t,而由(2)中结论可知PG=﹣t2+4t,于是建立方程解出t的值,P、Q坐标也就是自然得出,最后待定系数法确定PQ解析式.
,得到PG=4﹣t,而由(2)中结论可知PG=﹣t2+4t,于是建立方程解出t的值,P、Q坐标也就是自然得出,最后待定系数法确定PQ解析式.
(1)设OA=m,则OC=4OA=4m,
∵B(4,0),所以OB=4,
∴AB=OA+OB=4+m,
∴S△ABC=![]() ABOC=2m(4+m)=24,
ABOC=2m(4+m)=24,
解得:m=2,
∴A(﹣2,0),C(0,8),
将A、C两点坐标代入y=﹣x2+bx+c得:
![]() ,
,
解得b=2,c=8,
∴抛物线的解析式为y=﹣x2+2x+8;
(2) ∵EG⊥PD,PD⊥AB,∠EOD=90°,
∴四边形ODGE为矩形,
∴EG=OD,
∵P为抛物线上一点,且横坐标为t,
∴P(t,﹣t2+2t+8),
∴PD=﹣t22t+8,OD=t,
∵A(﹣2,0),
∴AD=t+2,
∵EG⊥PD,
∴△PEGPAD,且EG=OD=t,
∴![]() ,
,
所以![]() ,
,
所以d=﹣t2+4t;
(3)∵PG=d=﹣t2+4t,PD=﹣t2+2t+8,
∴GD=PD﹣PG=8﹣2t,
∴OE=BF=GD=8﹣2t,
设∠QMF=α,则∠MQF=90°﹣α,
∵∠DQM=45°,
∴∠GQD=180°﹣∠DQM﹣∠MQF=45°+α,
∴∠DQH=∠GQD=45°+α,
∴∠HQM=∠DQH﹣∠DQM=α,
根据折叠的性质∠H=∠QGD=90![]() =∠F,
=∠F,
∴Rt△QFM≌Rt△MHQ,
∴QH=MF,MH=QF,
如图,作MK⊥QM交DQ于K,过点K作SR⊥FB于R交GD于S,
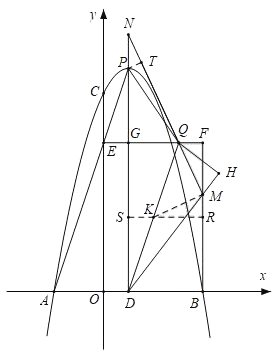
则∠KRM=∠KMQ=∠QFM=90°,
∵∠DQM=45°,
∴∠MKQ=45°=∠MQK,
∴QM=KM,
∵∠QMF+∠KMR=∠KMR+∠MKR=90°,
∴∠QMF=∠MKR,
∴Rt△QFM≌Rt△MRK,
∴KR=MF,MR=QF,
设QF=m,则MR=QF=m,
∴GQ=QH=FM=EF﹣EG﹣QF=4﹣t﹣m,
∴FR=FM+MR=4﹣t﹣m+m=4﹣t=![]() BF,
BF,
∵BF=GD=8﹣2t,
∴FR=![]() BF,
BF,
∴R为BF中点,
∴SK=![]() GQ,
GQ,
∵SK=SR﹣KR=GF﹣GQ=QF,
∴QF=![]() FM,
FM,
∴tan∠QMF=tanα=![]() ,
,
作PT⊥NQ于T,则tan∠N=![]() =tanα=
=tanα=![]() ,
,
∴NT=2PT,
∵tan∠PQN=![]()
![]() ,
,
∴QT=8PT,
设PT=n,则NT=2n,QT=8n,QN=10n,PN=![]() =
=![]() n,
n,
∵![]() =tan∠N=
=tan∠N=![]() ,
,
∴NG=2QG,
∵![]() ,即
,即![]() ,
,
∴![]() ,NG=2QG=4
,NG=2QG=4![]() n,
n,
∴PG=NG﹣PN=3![]() n,
n,
∴![]() =
=![]() ,
,
∵GQ=2SK=2QF=2m,
∴![]() ,
,
∴PG=GF=4﹣t,
又∵PG=﹣t2+4t,
∴﹣t2+4t=4﹣t,
∴t2﹣5t+4=0,解得t=1或t=5(舍),
∴P(1,9),Q(3,6),
设直线PQ的解析式为![]() ,
,
则![]() ,
,
解得: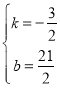 ,
,
∴PQ的解析式为y=﹣![]() x+
x+![]() .
.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
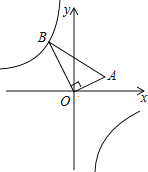
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( )
A.﹣2B.﹣4C.4D.﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题:
材料一:我们将![]() 与
与![]() 称为一对“对偶式”因为
称为一对“对偶式”因为![]() ,所以构造“对俩式”相乘可以有效地将
,所以构造“对俩式”相乘可以有效地将![]() 和
和![]() 中的
中的![]() 去掉.例如:已知
去掉.例如:已知![]() ,求
,求![]()
![]() 的值.解:
的值.解:![]() ,
,![]()
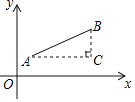
材料二:如图,点![]() ,点
,点![]() ,以AB为斜边作
,以AB为斜边作![]() ,则
,则![]() ,于是
,于是![]() ,
,![]() ,所以
,所以![]() .反之,可将代数式
.反之,可将代数式![]() 的值看作点
的值看作点![]() 到点
到点![]() 的距离.
的距离.
例如:![]() =
=![]() .
.
所以可将代数式![]() 的值看作点
的值看作点![]() 到点
到点![]() 的距离.
的距离.
![]() 利用材料一,解关于x的方程:
利用材料一,解关于x的方程:![]() ,其中
,其中![]() ;
;
![]() 利用材料二,求代数式
利用材料二,求代数式![]() 的最小值,并求出此时y与x的函数关系式,写出x的取值范图;
的最小值,并求出此时y与x的函数关系式,写出x的取值范图;
![]() 将
将![]() 所得的y与x的函数关系式和x的取值范围代入
所得的y与x的函数关系式和x的取值范围代入![]() 中解出x,直接写出x的值.
中解出x,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
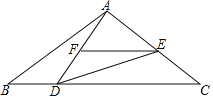
【题目】如图:已知在△ABC中,AB=AC,点D是BC上一点,∠ADE=∠B,
(1)求证:△ABD~△DCE;
(2)点F在AD上,且![]() =
=![]() ,求证:EF∥CD.
,求证:EF∥CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
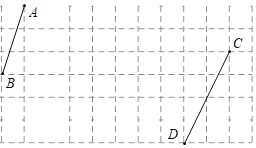
【题目】如图,在毎个小正方形的边长均为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上.
(1)画出一个以AB为一直角边的Rt△ABE,点E在小正方形的顶点上,且∠BAE=45°;
(2)画出一个以CD为一边的菱形CDMN,点M、N均在小正方形的顶点上,且菱形CDMN的面积是△ABE面积的4倍,连接EN,请直接写出线段EN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y1=-x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点
交于点A(1,m),这两条直线分别与x轴交于B,C两点
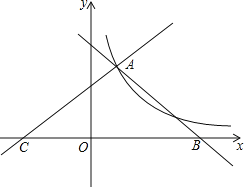
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
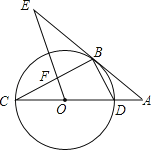
【题目】如图,CD是⊙O的直径,点B在⊙O上,连接BC、BD,直线AB与CD的延长线相交于点A,AB2=ADAC,OE∥BD交直线AB于点E,OE与BC相交于点F.
(1)求证:直线AE是⊙O的切线;
(2)若⊙O的半径为3,cosA=![]() ,求OF的长.
,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
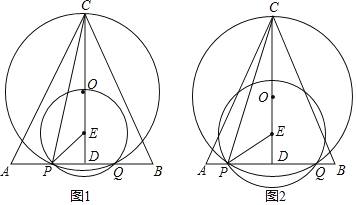
【题目】△ABC中,CA=CB,AB=![]() ,CD⊥AB于点D,CD=5,点O和点E在线段CD上,ED=1,点P在边AB上,以E为圆心,EP为半径的圆与AB边的另一个交点为点Q(点P在点Q的左侧),以O为圆心,OC为半径的圆O恰好经过P、Q两点,联结CP,设线段AP的长度为x.
,CD⊥AB于点D,CD=5,点O和点E在线段CD上,ED=1,点P在边AB上,以E为圆心,EP为半径的圆与AB边的另一个交点为点Q(点P在点Q的左侧),以O为圆心,OC为半径的圆O恰好经过P、Q两点,联结CP,设线段AP的长度为x.
(1)当圆E恰好经过点O时,求圆E的半径;
(2)联结CQ,设∠PCQ的正切值为y,求y与x的函数关系式及定义域;
(3)若∠PED=3∠PCE,求S△PCQ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com