
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( )
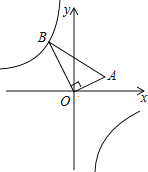
A.﹣2B.﹣4C.4D.﹣8
科目:初中数学 来源: 题型:
【题目】游泳是一项深受青少年喜爱的体育运动,某中学为了加强学生的游泳安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的![]() 名学生中作了抽样调查.制作了下面两个不完整的统计图.请根据这两个统计图回答以下问题:
名学生中作了抽样调查.制作了下面两个不完整的统计图.请根据这两个统计图回答以下问题:

(I)这次抽样调查中,共调查了 名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校![]() 名学生中大约有多少人“结伴时会下河学游泳”?
名学生中大约有多少人“结伴时会下河学游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC,以 AB 为直径的⊙O 与 BC 相交于点 D, 与 CA 的延长线相交于点 E,过点 D 作 DF⊥AC 于点 F.
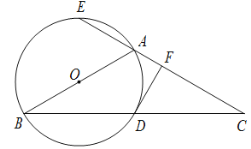
(1)试说明 DF 是⊙O 的切线;
(2)①当∠C= °时,四边形 AODF 为矩形;
②当 tanC= 时,AC=3AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
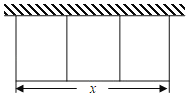
【题目】某农场拟用总长为60m的建筑材料建三间矩形牛饲养室,饲养室的一面靠现有墙(墙长为40m),其中间用建筑材料做的墙隔开(如图).设三间饲养室平行于墙的一边合计用建筑材料xm,总占地面积为ym2.
(1)求y关于x的函数解析式和自变量的取值范围;
(2)当x为何值时,三间饲养室占地总面积最大?最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
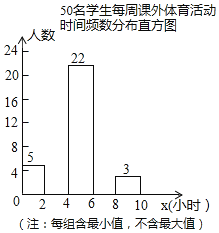
【题目】为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
(1)本次调查样本容量是 ;
(2)请补全频数分布直方图中空缺的部分;
(3)估计全校学生每周课外体育活动时间不少于6小时的人数.
(4)求这50名学生每周课外体育活动时间的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】距离中考体考时间越来越近,年级组想了解初三年级2400名学生周末在家体育锻炼的情况,在初三年级随机抽查了20名男生和20名女生周末每天在家锻炼的时间情况.
(一)收集数据:(单位:分)
男生:20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
女生:75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
(二)整理、描述数据:(表一)
时间x | x≤30 | 30<x≤60 | 60<x≤90 | 90<x≤120 |
男生 | 2 | 8 | 8 | 2 |
女生 | 1 | 4 | a | 3 |
(表二)两组数据的极差、平均数、中位数、众数
极差 | 平均数 | 中位数 | 众数 | |
男生 | 100 | 65.75 | b | c |
女生 | 90 | 75.5 | 75 | 75 |
(三)分析、应用数据:
(1)请将上面两个表格补充完整:a=_____,b=______,c=______;
(2)请根据抽样调查的数据估计初三年级周末每天锻炼时间在100分钟以上(含100分钟)的同学大约有多少人?
(3)李老师看了表格数据后认为初三年级的女生周末锻炼坚持得比男生好,请你结合统计数据,写出支持老师观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三年级有四个班,每班挑选乒乓球男女队员各一人,组成年级混合双打代表队,那么四对混合双打中,没有一队选手是同班同学的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c交x轴负半轴于点A,交x轴正半轴于点B(4,0),交y轴正半轴于点C,OC=4OA,S△ABC=24.
(1)求抛物线的解析式;
(2)点P为第一象限抛物线上一点,过点P作PD⊥AB于点D,连接AP交y轴于点E,过点E作EG⊥PD于点G,设点P的横坐标为t(t≤1),PG的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点B作BF⊥EG交EG的延长线于点F,点Q在线段GF上,连接DQ、PQ,将△DGQ沿DQ折叠后,点G的对称点为点H,DH交BF于点M,连接MQ并延长交DP的延长线于点N,当∠DQM=45°,tan∠PQN=![]() 时,求直线PQ的解析式.
时,求直线PQ的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
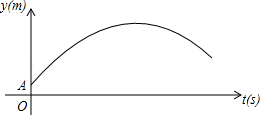
【题目】如图,某足球运动员站在点O处练习射门.将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,己知足球飞行0.8s时,离地面的高度为3.5m.
(1)a= ,c= ;
(2)当足球飞行的时间为多少时,足球离地面最高?最大高度是多少?
(3)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com