
【题目】距离中考体考时间越来越近,年级组想了解初三年级2400名学生周末在家体育锻炼的情况,在初三年级随机抽查了20名男生和20名女生周末每天在家锻炼的时间情况.
(一)收集数据:(单位:分)
男生:20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
女生:75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
(二)整理、描述数据:(表一)
时间x | x≤30 | 30<x≤60 | 60<x≤90 | 90<x≤120 |
男生 | 2 | 8 | 8 | 2 |
女生 | 1 | 4 | a | 3 |
(表二)两组数据的极差、平均数、中位数、众数
极差 | 平均数 | 中位数 | 众数 | |
男生 | 100 | 65.75 | b | c |
女生 | 90 | 75.5 | 75 | 75 |
(三)分析、应用数据:
(1)请将上面两个表格补充完整:a=_____,b=______,c=______;
(2)请根据抽样调查的数据估计初三年级周末每天锻炼时间在100分钟以上(含100分钟)的同学大约有多少人?
(3)李老师看了表格数据后认为初三年级的女生周末锻炼坚持得比男生好,请你结合统计数据,写出支持老师观点的理由.
【答案】(1)12,65,90;(2)每天运动时间在100分钟以上的同学大约有300人;(3)见解析.
【解析】
(1)根据中位数和众数的定义即可得到结论;
(2)根据表中数据计算即可;
(3)由表中数据即可看出李老师的观点正确.
解:(1)由题意可得:a=12;
20名男生周末每天的运动时间按从小到大的顺序排列为:20 30 40 40 45 45 50 50 50 60 70 70 80 85 90 90 90 90 100 120,
处在中间的两个数为60和70,
∴b=![]() =65;
=65;
∵90出现的次数最多,
∴c=90;
故答案为:12,65,90;
(2)由题意可得:2400×![]() =300(人)
=300(人)
答:初三年级周末每天运动时间在100分钟以上的同学大约有300人;
(3)①因为女生周末运动时间的平均数大于男生;
②因为女生周末运动时间的中位数大于男生.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 边长是定值,点
边长是定值,点![]() 是它的外心,过点
是它的外心,过点![]() 任意作一条直线分别交
任意作一条直线分别交![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 折叠,得到
折叠,得到![]() ,若
,若![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() ,则下列判断错误的是( )
,则下列判断错误的是( )
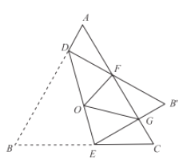
A.△![]() ≌△
≌△![]()
B.![]() 的周长是一个定值
的周长是一个定值
C.四边形![]() 的面积是一个定值
的面积是一个定值
D.四边形![]() 的面积是一个定值
的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
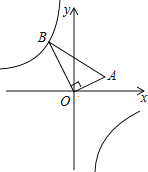
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( )
A.﹣2B.﹣4C.4D.﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D,B(﹣3,0),A(0,
x2+bx+c与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D,B(﹣3,0),A(0,![]() )
)
(1)求抛物线解析式及D点坐标;
(2)如图1,P为线段OB上(不与O、B重舍)一动点,过点P作y轴的平行线交线段AB于点M,交抛物线于点N,点N作NK⊥BA交BA于点K,当△MNK与△MPB的面积相等时,在X轴上找一动点Q,使得![]() CQ+QN最小时,求点Q的坐标及
CQ+QN最小时,求点Q的坐标及![]() CQ+QN最小值;
CQ+QN最小值;
(3)如图2,在(2)的条件下,将△ODN沿射线DN平移,平移后的对应三角形为△O′D′N′,将△AOC绕点O逆时针旋转到A1OC1的位置,且点C1恰好落在AC上,△A1D′N′是否能为等腰三角形,若能求出N′的坐标,若不能,请说明理由.
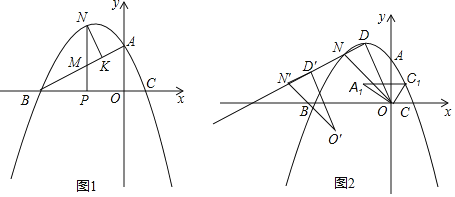
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题:
材料一:我们将![]() 与
与![]() 称为一对“对偶式”因为
称为一对“对偶式”因为![]() ,所以构造“对俩式”相乘可以有效地将
,所以构造“对俩式”相乘可以有效地将![]() 和
和![]() 中的
中的![]() 去掉.例如:已知
去掉.例如:已知![]() ,求
,求![]()
![]() 的值.解:
的值.解:![]() ,
,![]()
材料二:如图,点![]() ,点
,点![]() ,以AB为斜边作
,以AB为斜边作![]() ,则
,则![]() ,于是
,于是![]() ,
,![]() ,所以
,所以![]() .反之,可将代数式
.反之,可将代数式![]() 的值看作点
的值看作点![]() 到点
到点![]() 的距离.
的距离.
例如:![]() =
=![]() .
.
所以可将代数式![]() 的值看作点
的值看作点![]() 到点
到点![]() 的距离.
的距离.
![]() 利用材料一,解关于x的方程:
利用材料一,解关于x的方程:![]() ,其中
,其中![]() ;
;
![]() 利用材料二,求代数式
利用材料二,求代数式![]() 的最小值,并求出此时y与x的函数关系式,写出x的取值范图;
的最小值,并求出此时y与x的函数关系式,写出x的取值范图;
![]() 将
将![]() 所得的y与x的函数关系式和x的取值范围代入
所得的y与x的函数关系式和x的取值范围代入![]() 中解出x,直接写出x的值.
中解出x,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
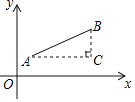
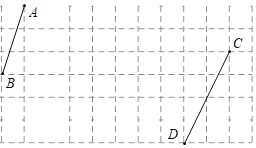
【题目】如图,在毎个小正方形的边长均为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上.
(1)画出一个以AB为一直角边的Rt△ABE,点E在小正方形的顶点上,且∠BAE=45°;
(2)画出一个以CD为一边的菱形CDMN,点M、N均在小正方形的顶点上,且菱形CDMN的面积是△ABE面积的4倍,连接EN,请直接写出线段EN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一放假期间,甲、乙、丙三位同学到某影城看电影,影城有A,B两部不同电影,甲、乙、丙3人分别从中任选一部观看,每部被选中的可能性相同.
(1)甲同学选择“A部电影”的概率为 ;
(2)用画树状图的方法求甲、乙、丙3人选择同一部电影的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com