
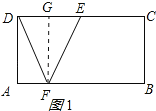
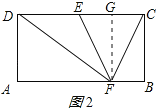
【题目】已知矩形ABCD,E为CD的中点,F为AB上一点,连接EF,DF,若AB=4,BC=2,EF=![]() ,则DF的长为_____.
,则DF的长为_____.
【答案】![]() 或
或![]()
【解析】
分两种情况:①点F靠近点A时,作FG⊥CD于G,则FG=BC=2,∠FGE=90°,由勾股定理求出GE,由矩形的性质和已知条件得出DG,由勾股定理求出DF的长;
②点F靠近点B时,作FG⊥CD于G,则FG=BC=2,∠FGE=90°,同①得出EG=1,得出DG=DE+EG=3,由勾股定理求出DF的长即可.
解:分两种情况:
①点F靠近点A时,如图1所示:
作FG⊥CD于G,
则FG=BC=2,∠FGE=90°,
∴GE=![]() =
=![]() =1,
=1,
∵四边形ABCD是矩形,
∴CD=AB=4,AD=BC=2,
∵E是CD的中点,
∴DE=![]() CD=2,
CD=2,
∴DG=2﹣1=1,
∴DF=![]() =
=![]() =
=![]() ;
;
②点F靠近点B时,如图2所示:
作FG⊥CD于G,
则FG=BC=2,∠FGE=90°,
同①得出EG=1,
∴DG=DE+EG=3,
∴DF=![]() =
=![]() =
=![]() ,
,
综上所述:DF的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 的一条弦,
的一条弦,![]() 是
是![]() 外一点,且
外一点,且![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() 和点
和点![]() ,连接
,连接![]() .
.
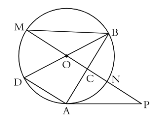
(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() 是
是![]() 的切线;
的切线;
(3)连接![]() ,若
,若![]() ,
,![]() .
.
①设![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ;
;
②求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,那么该商店至少要购进A种纪念品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
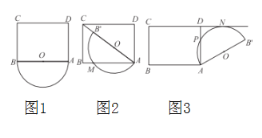
【题目】在矩形![]() 中,
中,![]() ,以
,以![]() 为直径的半圆
为直径的半圆![]() 在矩形
在矩形![]() 的外部,如图1,将半圆
的外部,如图1,将半圆![]() 绕点
绕点![]() 顺时针旋转α度(0°≤ɑ≤180°).
顺时针旋转α度(0°≤ɑ≤180°).
(1)在旋转过程中,![]() 的最小值是_____________,当半圆
的最小值是_____________,当半圆![]() 的直径落在对角线
的直径落在对角线![]() 上时,如图2,设半圆
上时,如图2,设半圆![]() 与
与![]() 的交点为
的交点为![]() ,则
,则![]() 长为__________.
长为__________.
(2)将半圆![]() 与直线
与直线![]() 相切时,切点为
相切时,切点为![]() ,半圆
,半圆![]() 与线段
与线段![]() 的交点为
的交点为![]() ,如图3,求劣弧
,如图3,求劣弧![]() 的长;
的长;
(3)在旋转过程中,当半圆弧与直线![]() 只有一个交点时,设此交点与点
只有一个交点时,设此交点与点![]() 的距离为
的距离为![]() 请直接写出
请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
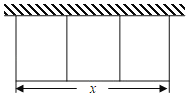
【题目】某农场拟用总长为60m的建筑材料建三间矩形牛饲养室,饲养室的一面靠现有墙(墙长为40m),其中间用建筑材料做的墙隔开(如图).设三间饲养室平行于墙的一边合计用建筑材料xm,总占地面积为ym2.
(1)求y关于x的函数解析式和自变量的取值范围;
(2)当x为何值时,三间饲养室占地总面积最大?最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
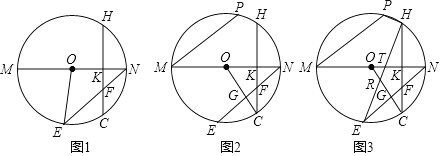
【题目】如图已知:MN为⊙O的直径,点E为弧MC上一点,连接EN交CH于点F,CH是⊙O的一条弦,CH⊥MN于点K.
(1)如图1,连接OE,求证:∠EON=2∠EFC;
(2)如图2,连接OC,OC与NE交于点G,若MP∥EN,MP=2HK,求证:FH=FE;
(3)如图3,在(2)的条件下,连接EH交OC与ON于点R,T,连接PH,若RT:RE=1:5,PH=2![]() ,求OR的长.
,求OR的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】距离中考体考时间越来越近,年级组想了解初三年级2400名学生周末在家体育锻炼的情况,在初三年级随机抽查了20名男生和20名女生周末每天在家锻炼的时间情况.
(一)收集数据:(单位:分)
男生:20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
女生:75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
(二)整理、描述数据:(表一)
时间x | x≤30 | 30<x≤60 | 60<x≤90 | 90<x≤120 |
男生 | 2 | 8 | 8 | 2 |
女生 | 1 | 4 | a | 3 |
(表二)两组数据的极差、平均数、中位数、众数
极差 | 平均数 | 中位数 | 众数 | |
男生 | 100 | 65.75 | b | c |
女生 | 90 | 75.5 | 75 | 75 |
(三)分析、应用数据:
(1)请将上面两个表格补充完整:a=_____,b=______,c=______;
(2)请根据抽样调查的数据估计初三年级周末每天锻炼时间在100分钟以上(含100分钟)的同学大约有多少人?
(3)李老师看了表格数据后认为初三年级的女生周末锻炼坚持得比男生好,请你结合统计数据,写出支持老师观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
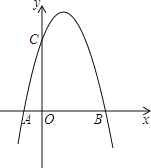
【题目】如图已知在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA.
(1)求点A坐标;
(2)求这条抛物线的解析式,并求出它的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 函数图象位于第一、三象限
B. 函数值y随x的增大而减小
C. 若A(-1,y1)、B(1,y2)、C(2,y3)是图象上三个点,则y1<y3<y2
D. P为图象上任意一点,过P作PQ⊥y轴于Q,则△OPQ的面积是定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com