
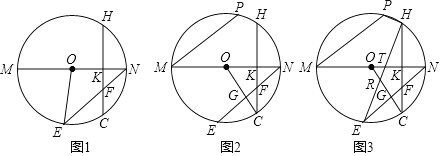
【题目】如图已知:MN为⊙O的直径,点E为弧MC上一点,连接EN交CH于点F,CH是⊙O的一条弦,CH⊥MN于点K.
(1)如图1,连接OE,求证:∠EON=2∠EFC;
(2)如图2,连接OC,OC与NE交于点G,若MP∥EN,MP=2HK,求证:FH=FE;
(3)如图3,在(2)的条件下,连接EH交OC与ON于点R,T,连接PH,若RT:RE=1:5,PH=2![]() ,求OR的长.
,求OR的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)由于MN是直径,于是连接EM,然后说明∠EMO=∠EFC即可;
(2)连接ME、EH、PN、EC、CN、HN,先证明△MPN≌△ENM,再证明∠CHE=∠NEH即可;
(3)由已知条件可以推出∠EOC=∠CON=∠HON,进而推出OR平分∠EOT,EG=HT,OR=OT,根据角平分线比例定理OT:OE=RT:RE=1:5,故设OT=OR=x,RT=y,则MT、TN可用x表示出来,TH、TE可用y表示出来,根据相交弦定理可以得出x与y关系式,将y用x表示出来,EH也就用x表示出来了,同时注意到PE是直径,且PE也用x表示出来,PH已知,利用勾股定理列方程即可解出x.
解:(1)如图1,连接EM,
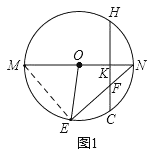
∵MN为圆O的直径,
∴∠MEN=90°,
∵CH⊥MN于K,
∴∠MKF=90°,
∴∠MEF+∠MKF=180°,
∴∠EFC=∠EMO,
∵OE=OM,
∴∠EON=2∠EMO=2∠EFC;
(2)如图2,连接ME、EH、PN、EC、CN、HN,
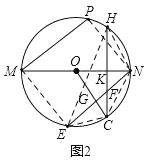
∵MN为圆O直径,
∴∠MPN=∠MEN=90°,
∵MP∥EN,
∴∠PMN=∠ENM,
∴△MPN≌△ENM(AAS),
∴MP=EN,
∵MN⊥CH于K,
∴KH=CK=![]() CH,HN=CN
CH,HN=CN
∴CH=2KH,∠HEN=∠CEN=∠NHC,
∵MP=2KH,
∴CH=MP=EN,
∴∠HEC=∠NHE,
∴∠HEN=∠EHC,
∴FH=FE;
(3)如图3,连接EM、PN、PE、CE、CN、HN、OH,
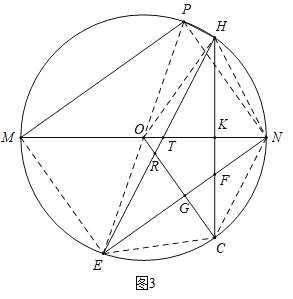
∵PM=EN且MP∥EN,∠MPN=90°,
∴四边形MENP是矩形,
∴PE为圆O直径,
∴∠PHE=∠PNE=90°,
∵∠ENC=∠EHC=∠HEN=∠HCN=∠NHC=∠CEN,
∴CE=CN,
∵OE=ON,
∴OC垂直平分EN,
∴∠EOC=∠NOC,
由角平分线比例定理可知: ![]() ,
,
∴设OT=x,则ON=OM=OP=OC=OE=5x,
∴MT=6x,TN=4x,
∵CE=CN=HN,
∴∠EOR=∠HOT,
∵OH=OE,
∴∠OEH=∠OHE,
∴△OER≌△OHT(ASA),
∴OR=OT=x,TH=RE,
设RT=y,则ER=HT=5y,ET=6y,
由相交弦定理有:MTTN=ETTH,
∴6x4x=6y5y,
∴4x2=5y2,
∴![]() ,
,
∴y=![]() x,
x,
∴EH=ER+RT+TH=11y=![]() x,
x,
在Rt△PHE中:PE2=PH2+EH2,
∴100x2=8+![]() ,
,
∴x2=![]() ,
,
∴x取正数,则x=![]() ,
,
∴OR=![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
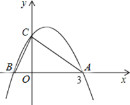
【题目】如图,抛物线![]() 与
与![]() 轴相交于点A(3,0)和
轴相交于点A(3,0)和![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)点D(x,y)是抛物线上一点,若S△ABD= S△ABC,求点![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
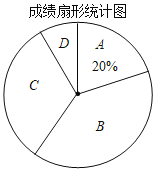
【题目】在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
成绩频数分布统计表
组别 | A | B | C | D |
成绩x(分) | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
人数 | 10 | m | 16 | 4 |
请观察上面的图表,解答下列问题:
(1)统计表中m= ,D组的圆心角为 °;
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国的经济总量已居世界第二,人民富裕了,有的家庭拥有多种车型.小红家有A、B、C三种车型,已知3辆A型车的载重量与4辆B型车的载重量之和刚好等于2辆C型车的载重量;4辆B型车的载重量与1辆C型车的载重量之和刚好等于6辆A型车的载重量.现有一批货物,原计划用C型车10次可全部运完,由于C型车另有运输任务,现在安排A型车单独装运12次,余下的货物由B型车单独装运刚好可以全部运完,则B型车需单独装运_____次(每辆车每次都满载重量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D,B(﹣3,0),A(0,
x2+bx+c与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D,B(﹣3,0),A(0,![]() )
)
(1)求抛物线解析式及D点坐标;
(2)如图1,P为线段OB上(不与O、B重舍)一动点,过点P作y轴的平行线交线段AB于点M,交抛物线于点N,点N作NK⊥BA交BA于点K,当△MNK与△MPB的面积相等时,在X轴上找一动点Q,使得![]() CQ+QN最小时,求点Q的坐标及
CQ+QN最小时,求点Q的坐标及![]() CQ+QN最小值;
CQ+QN最小值;
(3)如图2,在(2)的条件下,将△ODN沿射线DN平移,平移后的对应三角形为△O′D′N′,将△AOC绕点O逆时针旋转到A1OC1的位置,且点C1恰好落在AC上,△A1D′N′是否能为等腰三角形,若能求出N′的坐标,若不能,请说明理由.
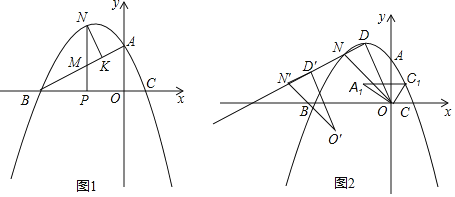
查看答案和解析>>
科目:初中数学 来源: 题型:
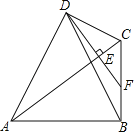
【题目】如图,四边形ABCD中,∠ADC=∠ABC=90°,连接AC、BD,作DF⊥AC,交AC于点E,交BC于点F,∠ADB=2∠DBC,若BC=![]() ,DF=5
,DF=5![]() ,则AB的长为_____.
,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】横、纵坐标均为整数的点叫做格点,例如A(1,4),B(1,1),C(4,1),D(4,4),E(2,1)都是格点.
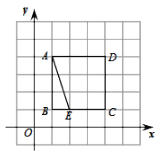
(1)取格点F,使得BF⊥AE,BF=AE;
(2)将线段BF绕点F顺时针旋转90°,得到线段FM;
(3)用无刻度的直尺在AD上取点N,使得FN=CF+AN,保留作图痕迹,并直接写出点F,M,N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com