
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½©![]() x2+bx+cÓėxÖį½»ÓŚB”¢CĮ½µć£ØµćBŌŚµćCµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćA£¬Å×ĪļĻߵĶ„µćĪŖD£¬B£Ø©3£¬0£©£¬A£Ø0£¬
x2+bx+cÓėxÖį½»ÓŚB”¢CĮ½µć£ØµćBŌŚµćCµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćA£¬Å×ĪļĻߵĶ„µćĪŖD£¬B£Ø©3£¬0£©£¬A£Ø0£¬![]() £©
£©
£Ø1£©ĒóÅ×ĪļĻß½āĪöŹ½¼°Dµć×ų±ź£»
£Ø2£©ČēĶ¼1£¬PĪŖĻ߶ĪOBÉĻ£Ø²»ÓėO”¢BÖŲÉį£©Ņ»¶Æµć£¬¹żµćP×÷yÖįµÄĘ½ŠŠĻß½»Ļ߶ĪABÓŚµćM£¬½»Å×ĪļĻßÓŚµćN£¬µćN×÷NK”ĶBA½»BAÓŚµćK£¬µ±”÷MNKÓė”÷MPBµÄĆ껿ĻąµČŹ±£¬ŌŚXÖįÉĻÕŅŅ»¶ÆµćQ£¬Ź¹µĆ![]() CQ+QN×īŠ”Ź±£¬ĒóµćQµÄ×ų±ź¼°
CQ+QN×īŠ”Ź±£¬ĒóµćQµÄ×ų±ź¼°![]() CQ+QN×īŠ”Öµ£»
CQ+QN×īŠ”Öµ£»
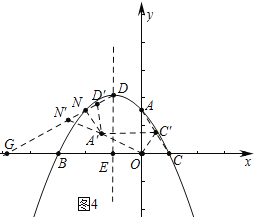
£Ø3£©ČēĶ¼2£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬½«”÷ODNŃŲÉäĻßDNĘ½ŅĘ£¬Ę½ŅĘŗóµÄ¶ŌӦȿ½ĒŠĪĪŖ”÷O”äD”äN”䣬½«”÷AOCČʵćOÄꏱÕėŠż×Ŗµ½A1OC1µÄĪ»ÖĆ£¬ĒŅµćC1Ē”ŗĆĀäŌŚACÉĻ£¬”÷A1D”äN”äŹĒ·ńÄÜĪŖµČŃüČż½ĒŠĪ£¬ČōÄÜĒó³öN”äµÄ×ų±ź£¬Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
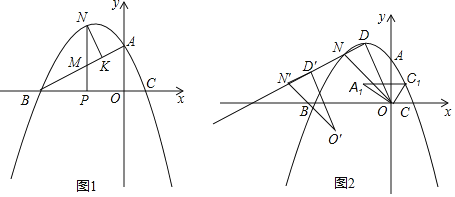
”¾“š°ø”æ£Ø1£©y£½©![]() x2©
x2©![]() x+
x+![]() £»¶„µćDµÄ×ų±źĪŖ£Ø©1£¬
£»¶„µćDµÄ×ų±źĪŖ£Ø©1£¬![]()
![]() £©£»£Ø2£©Q£Ø©1£¬0£©£¬×īŠ”ÖµĪŖ3£»£Ø3£©N”äµÄ×ų±źĪŖ£Ø©
£©£»£Ø2£©Q£Ø©1£¬0£©£¬×īŠ”ÖµĪŖ3£»£Ø3£©N”äµÄ×ų±źĪŖ£Ø©![]() £¬
£¬![]() £©»ņ£Ø©
£©»ņ£Ø©![]() £¬
£¬![]() £©£®
£©£®
”¾½āĪö”æ
£Ø1£©ĄūÓĆ“ż¶ØĻµŹż·ØŅŌ¼°¶„µć×ų±ź¹«Ź½¼“æɽā¾öĪŹĢā£®
£Ø2£©ČēĶ¼1ÖŠ£¬ÉčP£Øm£¬0£©ŌņN£Øm£¬©![]() m2©
m2©![]() m+
m+![]() £©£®ÓÉ”÷NMK”×”÷BMN£¬ÓÖ”÷MNKÓė”÷MPBµÄĆ껿ĻąµČ£¬ĶĘ³ö”÷NMK”Õ”÷BMN£¬ĶĘ³öMN£½BM£¬ŌŚRt”÷ABOÖŠ£¬tan”ĻABO£½
£©£®ÓÉ”÷NMK”×”÷BMN£¬ÓÖ”÷MNKÓė”÷MPBµÄĆ껿ĻąµČ£¬ĶĘ³ö”÷NMK”Õ”÷BMN£¬ĶĘ³öMN£½BM£¬ŌŚRt”÷ABOÖŠ£¬tan”ĻABO£½![]() £½
£½![]() £¬ĶĘ³ö”ĻABO£½30”ć£¬ĶĘ³öBM£½2PM£½MN£¬æɵƩ
£¬ĶĘ³ö”ĻABO£½30”ć£¬ĶĘ³öBM£½2PM£½MN£¬æɵƩ![]() m2©
m2©![]() m+
m+![]() ©
©![]() m+
m+![]() £½2£Ø
£½2£Ø![]() m+
m+![]() £©£¬½āµĆm£½©2»ņ©3£ØÉįĘś£©£¬ĶĘ³öN£Ø©2£¬
£©£¬½āµĆm£½©2»ņ©3£ØÉįĘś£©£¬ĶĘ³öN£Ø©2£¬![]() £©£¬
£©£¬
ŌŚyÖįÉĻČ”Ņ»µćF£¬Ź¹µĆ”ĻOCF£½30”ć£¬×÷QH”ĶCFÓŚH£¬ŅņĪŖQH£½![]() CQ£¬ĖłŅŌNQ+
CQ£¬ĖłŅŌNQ+![]() CQ£½NQ+QH£¬øł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬µ±N”¢Q”¢H¹²Ļߣ¬ĒŅNH”ĶCFŹ±£¬NQ+
CQ£½NQ+QH£¬øł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬µ±N”¢Q”¢H¹²Ļߣ¬ĒŅNH”ĶCFŹ±£¬NQ+![]() CQ£½NQ+QHµÄÖµ×īŠ”£®ÓÉ“Ė¼“æɽā¾öĪŹĢā£®
CQ£½NQ+QHµÄÖµ×īŠ”£®ÓÉ“Ė¼“æɽā¾öĪŹĢā£®
£Ø3£©Ź×ĻČĒó³öµćA”äµÄ×ų±ź£¬ŌŁÖ¤Ć÷A”äN”ĶDN£¬·ÖČżÖÖĒéŠĪĢÖĀŪ¼“æÉ£®¢ŁČēĶ¼3ÖŠ£¬µ±A”äD”䣽A”äN”䏱£®¢ŚČēĶ¼4ÖŠ£¬µ±N”äD”䣽N”äA”䏱£®¢ŪČēĶ¼5ÖŠ£¬ŃÓ³¤C”äA”ä½»DGÓŚN”䣬“ĖŹ±”÷D”äN”äA”äŹĒµČŃüČż½ĒŠĪ£®
½ā£ŗ£Ø1£©°ŃB£Ø©3£¬0£©£¬A£Ø0£¬![]() £©µÄ×ų±ź“śČėy£½©
£©µÄ×ų±ź“śČėy£½©![]() x2+bx+c£¬µĆµ½
x2+bx+c£¬µĆµ½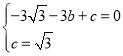 £¬
£¬
½āµĆ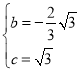 £¬
£¬
”ą¶ž“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy£½©![]() x2©
x2©![]() x+
x+![]() £¬
£¬
¶„µćDµÄ×ų±źĪŖ£Ø©1£¬![]()
![]() £©£®
£©£®
£Ø2£©ČēĶ¼1ÖŠ£¬ÉčP£Øm£¬0£©ŌņN£Øm£¬![]() £©£®
£©£®
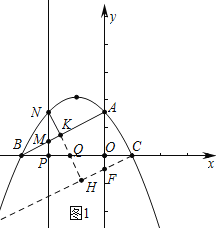
”ßA£Ø0£¬![]() £©£¬B£Ø©3£¬0£©£¬
£©£¬B£Ø©3£¬0£©£¬
”ąÖ±ĻßABµÄ½āĪöŹ½ĪŖy£½![]() x+
x+![]() £¬ABÓĆPNµÄ½»µćM£Øm£¬
£¬ABÓĆPNµÄ½»µćM£Øm£¬![]() m+
m+![]() £©£¬
£©£¬
”ß”ĻNMK£½”ĻBMP£¬”ĻNKM£½”ĻMPB£½90”ć£¬
”ą”÷NMK”×”÷BMN£¬
”ß”÷MNKÓė”÷MPBµÄĆ껿ĻąµČ£¬
”ą”÷NMK”Õ”÷BMN£¬
”ąMN£½BM£¬
ŌŚRt”÷ABOÖŠ£¬tan”ĻABO£½![]() £½
£½![]() £¬
£¬
”ą”ĻABO£½30”ć£¬
”ąBM£½2PM£½MN£¬
”ą©![]() m2©
m2©![]()
![]() m+
m+![]() ©
©![]() m+
m+![]() £½2£Ø
£½2£Ø![]() m+
m+![]() £©£¬
£©£¬
½āµĆm£½©2»ņ©3£ØÉįĘś£©£¬
”ąN£Ø©2£¬![]() £©£¬
£©£¬
ŌŚyÖįÉĻČ”Ņ»µćF£¬Ź¹µĆ”ĻOCF£½30”ć£¬×÷QH”ĶCFÓŚH£¬
”ßQH£½![]() CQ£¬
CQ£¬
”ąNQ+![]() CQ£½NQ+QH£¬
CQ£½NQ+QH£¬
øł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬µ±N”¢Q”¢H¹²Ļߣ¬ĒŅNH”ĶCFŹ±£¬NQ+![]() CQ£½NQ+QHµÄÖµ×īŠ”£®
CQ£½NQ+QHµÄÖµ×īŠ”£®
”ßÖ±ĻßCFµÄ½āĪöŹ½ĪŖy£½![]() x©
x©![]() £¬Ö±ĻßNHµÄ½āĪöŹ½ĪŖy£½©
£¬Ö±ĻßNHµÄ½āĪöŹ½ĪŖy£½©![]() x©
x©![]() £¬
£¬
”ąQ£Ø©1£¬0£©£¬
ÓÉ £¬½āµĆ
£¬½āµĆ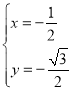 £¬
£¬
”ąH£Ø©![]() £¬©
£¬©![]() £©£¬
£©£¬
”ąNH£½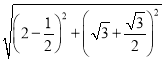 £½3£¬
£½3£¬
”ąNQ+![]() CQ£½NQ+QHµÄ×īŠ”ÖµĪŖ3£®
CQ£½NQ+QHµÄ×īŠ”ÖµĪŖ3£®
£Ø3£©ČēĶ¼2ÖŠ£¬
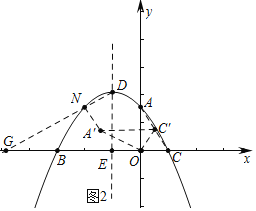
ŌŚRt”÷AOCÖŠ£¬”ßOA£½![]() £¬OC£½1£¬AC£½2£¬
£¬OC£½1£¬AC£½2£¬
”ątan”ĻACO£½![]() £¬
£¬
”ą”ĻACO£½60”ć£¬
”ßOC”䣽OC£¬
”ą”÷COC”äŹĒµČ±ßČż½ĒŠĪ£¬
”ą”ĻA”äC”äC£½”ĻC”äOC£½60”ć£¬
”ąA”äC”ä”ĪOC£¬
”ąA”ä£Ø©![]() £¬
£¬![]() £©£¬
£©£¬
”ßN£Ø©2£¬![]() £©£¬D£Ø©1£¬
£©£¬D£Ø©1£¬![]()
![]() £©£¬
£©£¬
”ąÖ±ĻßDNµÄ½āĪöŹ½ĪŖy£½![]() x+
x+![]()
![]() £¬Ö±ĻßA”äNµÄ½āĪöŹ½y£½©
£¬Ö±ĻßA”äNµÄ½āĪöŹ½y£½©![]() x©
x©![]() £¬
£¬
”ß![]() ”Į£Ø©
”Į£Ø©![]() £©£½©1£¬
£©£½©1£¬
”ąAN”ĶDN£¬ÉčÖ±ĻßDN½»xÖįÓŚG£¬ŌņG£Ø©5£¬0£©£¬¶Ō³ĘÖįÓėxÖįµÄ½»µćĪŖE£Ø©1£¬0£©£¬
ŌŚRt”÷DGEÖŠ£¬tan”ĻDGE£½![]() £¬
£¬
”ą”ĻDGE£½30”ć£®
¢ŁČēĶ¼3ÖŠ£¬µ±A”äD”䣽A”äN”䏱£¬Ņ×ÖŖND”䣽NN”䣬A”äN£½1£¬ND”䣽NN”䣽![]() £¬Ņ×Ö¤”÷A”äN”äD”äŹĒµČ±ßČż½ĒŠĪ£¬æɵĆN”ä£Ø©
£¬Ņ×Ö¤”÷A”äN”äD”äŹĒµČ±ßČż½ĒŠĪ£¬æɵĆN”ä£Ø©![]() £¬
£¬![]() £©£®
£©£®
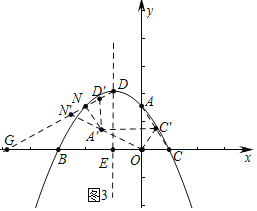
¢ŚČēĶ¼4ÖŠ£¬µ±N”äD”䣽N”äA”䏱£¬”ßA”äN£½1£¬DN£½![]() £¬
£¬
ŌŚRt”÷A”äN”äNÖŠ£¬A”äN”䣽N”äD”䣽![]() £¬A”äN£½1£¬NN”䣽
£¬A”äN£½1£¬NN”䣽![]() £¬Ņ×Ö¤”÷A”äN”äD”äŹĒµČ±ßČż½ĒŠĪ£¬
£¬Ņ×Ö¤”÷A”äN”äD”äŹĒµČ±ßČż½ĒŠĪ£¬
”ąN”ä£Ø©![]() £¬
£¬![]() £©£®
£©£®
¢ŪČēĶ¼5ÖŠ£¬ŃÓ³¤C”äA”ä½»DGÓŚN”䣬“ĖŹ±”÷D”äN”äA”äŹĒµČŃüČż½ĒŠĪ£®
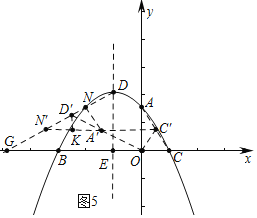
ĄķÓÉ£ŗ×÷D”äK”ĶC”äN”äÓŚK£¬Ņ×ÖŖN”ä£Ø©![]() £¬
£¬![]() £©£¬
£©£¬
”ąA”äN”䣽2£¬
ŌŚRt”÷D”äN”äKÖŠ£¬”ß”ĻD”äN”äK£½30”ć£¬D”äN”䣽![]() £¬
£¬
”ąD”äK£½![]() £¬KN”䣽1£¬
£¬KN”䣽1£¬
”ąKA”䣽A”äN”ä©N”äK£½2©1£½1£¬
ŌŚRt”÷A”äD”äKÖŠ£¬A”äD”䣽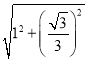 £½
£½![]() £¬
£¬
”ąD”äN”䣽D”äA”䣬
”ą”÷A”äD”äN”äŹĒµČŃüČż½ĒŠĪ£¬
×ŪÉĻĖłŹö£¬µ±µćN”äµÄ×ų±źĪŖ£Ø©![]() £¬
£¬![]() £©»ņ£Ø©
£©»ņ£Ø©![]() £¬
£¬![]() £©Ź±£¬”÷A”äD”äN”äŹĒµČŃüČż½ĒŠĪ£®
£©Ź±£¬”÷A”äD”äN”äŹĒµČŃüČż½ĒŠĪ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»“ĪĻņʶĄ§É½Ēųѧɜ”°°®ŠÄ֜ѧ”±¾čæī»ī¶ÆÖŠ£¬Ä³Š£Ń§ÉśČĖČĖÄĆ³ö×Ō¼ŗµÄĮć»ØĒ®Ó»Ō¾¾čæī£¬Ń§Éś¾čæī¶īÓŠ5ŌŖ”¢10ŌŖ”¢15ŌŖ”¢20ŌŖĖÄÖÖĒéæö£¬øł¾ŻĖ껜³éŃłĶ³¼ĘŹż¾Ż»ęÖĘĮĖĶ¼¢ŁŗĶĶ¼¢ŚĮ½·łÉŠ²»ĶźÕūµÄĶ³¼ĘĶ¼£®ĒėÄćøł¾ŻĶ¼ÖŠŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
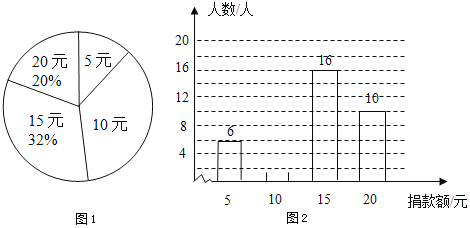
£Ø1£©Ēó³ö±¾“Ī³éŃłµÄѧɜČĖŹż²¢Ēó¾čæī¶īĪŖ5ŌŖµÄѧɜČĖŹżÕ¼³éŃłČĖŹżµÄ°Ł·Ö±Č£æ
£Ø2£©ĒėÄć½«Ķ¼¢ŚµÄĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©ČōøĆŠ£¾ÅÄź¼¶ČĖŹżĪŖ600ČĖ£¬ĒėÄć¹Ą¼ĘøĆŠ£¾ÅÄź¼¶Ņ»¹²¾čæī¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬ŅŌ
£¬ŅŌ![]() ĪŖÖ±¾¶µÄ°ėŌ²
ĪŖÖ±¾¶µÄ°ėŌ²![]() ŌŚ¾ŲŠĪ
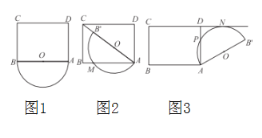
ŌŚ¾ŲŠĪ![]() µÄĶā²æ£¬ČēĶ¼1£¬½«°ėŌ²
µÄĶā²æ£¬ČēĶ¼1£¬½«°ėŌ²![]() Čʵć
Čʵć![]() Ė³Ź±ÕėŠż×Ŗ¦Į¶Č£Ø0”ć”ÜØ»”Ü180”ć£©£®
Ė³Ź±ÕėŠż×Ŗ¦Į¶Č£Ø0”ć”ÜØ»”Ü180”ć£©£®
£Ø1£©ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬![]() µÄ×īŠ”ÖµŹĒ_____________£¬µ±°ėŌ²
µÄ×īŠ”ÖµŹĒ_____________£¬µ±°ėŌ²![]() µÄÖ±¾¶ĀäŌŚ¶Ō½ĒĻß
µÄÖ±¾¶ĀäŌŚ¶Ō½ĒĻß![]() ÉĻŹ±£¬ČēĶ¼2£¬Éč°ėŌ²
ÉĻŹ±£¬ČēĶ¼2£¬Éč°ėŌ²![]() Óė
Óė![]() µÄ½»µćĪŖ
µÄ½»µćĪŖ![]() £¬Ōņ
£¬Ōņ![]() ³¤ĪŖ__________£®
³¤ĪŖ__________£®
£Ø2£©½«°ėŌ²![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() ĻąĒŠŹ±£¬ĒŠµćĪŖ
ĻąĒŠŹ±£¬ĒŠµćĪŖ![]() £¬°ėŌ²
£¬°ėŌ²![]() ÓėĻ߶Ī
ÓėĻ߶Ī![]() µÄ½»µćĪŖ
µÄ½»µćĪŖ![]() £¬ČēĶ¼3£¬ĒóĮÓ»”
£¬ČēĶ¼3£¬ĒóĮÓ»”![]() µÄ³¤£»
µÄ³¤£»
£Ø3£©ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±°ėŌ²»”ÓėÖ±Ļß![]() Ö»ÓŠŅ»øö½»µćŹ±£¬Éč“Ė½»µćÓėµć
Ö»ÓŠŅ»øö½»µćŹ±£¬Éč“Ė½»µćÓėµć![]() µÄ¾ąĄėĪŖ
µÄ¾ąĄėĪŖ![]() ĒėÖ±½ÓŠ“³ö
ĒėÖ±½ÓŠ“³ö![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
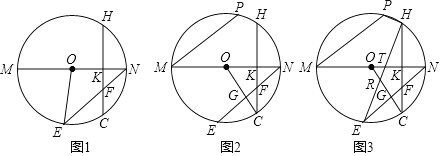
”¾ĢāÄæ”æČēĶ¼ŅŃÖŖ£ŗMNĪŖ”ŃOµÄÖ±¾¶£¬µćEĪŖ»”MCÉĻŅ»µć£¬Į¬½ÓEN½»CHÓŚµćF£¬CHŹĒ”ŃOµÄŅ»ĢõĻŅ£¬CH”ĶMNÓŚµćK£®
£Ø1£©ČēĶ¼1£¬Į¬½ÓOE£¬ĒóÖ¤£ŗ”ĻEON£½2”ĻEFC£»
£Ø2£©ČēĶ¼2£¬Į¬½ÓOC£¬OCÓėNE½»ÓŚµćG£¬ČōMP”ĪEN£¬MP£½2HK£¬ĒóÖ¤£ŗFH£½FE£»
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½ÓEH½»OCÓėONÓŚµćR£¬T£¬Į¬½ÓPH£¬ČōRT£ŗRE£½1£ŗ5£¬PH£½2![]() £¬ĒóORµÄ³¤£®
£¬ĒóORµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¾ąĄėÖŠæ¼Ģåæ¼Ź±¼äŌ½Ą“Ō½½ü£¬Äź¼¶×éĻėĮĖ½ā³õȿğ¼¶2400ĆūѧɜÖÜÄ©ŌŚ¼ŅĢåÓż¶ĶĮ¶µÄĒéæö£¬ŌŚ³õȿğ¼¶Ė껜³é²éĮĖ20ĆūÄŠÉśŗĶ20ĆūÅ®ÉśÖÜÄ©ĆæĢģŌŚ¼Ņ¶ĶĮ¶µÄŹ±¼äĒéæö£®
£ØŅ»£©ŹÕ¼ÆŹż¾Ż£ŗ£Øµ„Ī»£ŗ·Ö£©
ÄŠÉś£ŗ20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
Å®Éś£ŗ75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
£Ø¶ž£©ÕūĄķ”¢ĆčŹöŹż¾Ż£ŗ£Ø±ķŅ»£©
Ź±¼äx | x”Ü30 | 30£¼x”Ü60 | 60£¼x”Ü90 | 90£¼x”Ü120 |
ÄŠÉś | 2 | 8 | 8 | 2 |
Å®Éś | 1 | 4 | a | 3 |
£Ø±ķ¶ž£©Į½×鏿¾ŻµÄ¼«²ī”¢Ę½¾łŹż”¢ÖŠĪ»Źż”¢ÖŚŹż
¼«²ī | Ę½¾łŹż | ÖŠĪ»Źż | ÖŚŹż | |
ÄŠÉś | 100 | 65.75 | b | c |
Å®Éś | 90 | 75.5 | 75 | 75 |
£ØČż£©·ÖĪö”¢Ó¦ÓĆŹż¾Ż£ŗ
£Ø1£©Ēė½«ÉĻĆęĮ½øö±ķøń²¹³äĶźÕū£ŗa£½_____£¬b£½______£¬c£½______£»
£Ø2£©Ēėøł¾Ż³éŃłµ÷²éµÄŹż¾Ż¹Ą¼Ę³õȿğ¼¶ÖÜÄ©ĆæĢģ¶ĶĮ¶Ź±¼äŌŚ100·ÖÖÓŅŌÉĻ£Øŗ¬100·ÖÖÓ£©µÄĶ¬Ń§“óŌ¼ÓŠ¶ąÉŁČĖ£æ
£Ø3£©ĄīĄĻŹ¦æ“ĮĖ±ķøńŹż¾ŻŗóČĻĪŖ³õȿ𼶵ÄÅ®ÉśÖÜÄ©¶ĶĮ¶¼į³ÖµĆ±ČÄŠÉśŗĆ£¬ĒėÄć½įŗĻĶ³¼ĘŹż¾Ż£¬Š“³öÖ§³ÖĄĻŹ¦¹ŪµćµÄĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĮāŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬ĮāŠĪ
£¬ĮāŠĪ![]() ŌŚÖ±Ļß
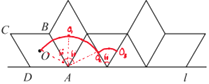
ŌŚÖ±Ļß![]() ÉĻĻņÓŅ×÷ĪŽ»¬¶ÆµÄ·¹ö£¬ĆæČĘ×ÅŅ»øö¶„µćŠż×Ŗ
ÉĻĻņÓŅ×÷ĪŽ»¬¶ÆµÄ·¹ö£¬ĆæČĘ×ÅŅ»øö¶„µćŠż×Ŗ![]() ½ŠŅ»“Ī²Ł×÷£¬Ōņ¾¹ż45“ĪÕāŃłµÄ²Ł×÷ĮāŠĪÖŠŠÄ
½ŠŅ»“Ī²Ł×÷£¬Ōņ¾¹ż45“ĪÕāŃłµÄ²Ł×÷ĮāŠĪÖŠŠÄ![]() Ėł¾¹żµÄĀ·¾¶×ܳ¤ĪŖ______£®£Ø½į¹ū±£Įō
Ėł¾¹żµÄĀ·¾¶×ܳ¤ĪŖ______£®£Ø½į¹ū±£Įō![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
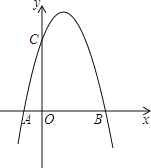
”¾ĢāÄæ”æČēĶ¼ŅŃÖŖŌŚÖ±½Ē×ų±źĻµÖŠ£¬Ņ»ĢõÅ×ĪļĻßÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚCµć£¬ĘäÖŠB£Ø3£¬0£©£¬C£Ø0£¬4£©£¬µćAŌŚxÖįµÄøŗ°ėÖįÉĻ£¬OC£½4OA£®
£Ø1£©ĒóµćA×ų±ź£»
£Ø2£©ĒóÕāĢõÅ×ĪļĻߵĽāĪöŹ½£¬²¢Ēó³öĖüµÄ¶„µć×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
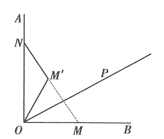
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬![]() £¬µć
£¬µć![]() ĪŖ
ĪŖ![]() ÄŚ²æŅ»µć£¬×÷ÉäĻß
ÄŚ²æŅ»µć£¬×÷ÉäĻß![]() £¬µć
£¬µć![]() ŌŚÉäĻß
ŌŚÉäĻß![]() ÉĻ£¬ĒŅ
ÉĻ£¬ĒŅ![]() £¬µć
£¬µć![]() Óėµć
Óėµć![]() ¹ŲÓŚÉäĻß
¹ŲÓŚÉäĻß![]() ¶Ō³Ę£¬ĒŅÖ±Ļß
¶Ō³Ę£¬ĒŅÖ±Ļß![]() ÓėÉäĻß
ÓėÉäĻß![]() ½»ÓŚµć
½»ÓŚµć![]() £®µ±
£®µ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬
ĪŖµČŃüČż½ĒŠĪŹ±£¬![]() µÄ³¤ĪŖ__________£®
µÄ³¤ĪŖ__________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
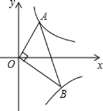
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćA”¢B·Ö±šŌŚ·“±ČĄżŗÆŹż![]() £¬
£¬![]() µÄĶ¼ĻóÉĻ£¬ĒŅOA
µÄĶ¼ĻóÉĻ£¬ĒŅOA![]() OB£¬ Ōņ
OB£¬ Ōņ![]() µÄÖµĪŖ ____________ £®
µÄÖµĪŖ ____________ £®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com