
����Ŀ����һ����ƶ��ɽ��ѧ����������ѧ������У�ijУѧ�������ó��Լ����㻨ǮӻԾ��ѧ��������5Ԫ��10Ԫ��15Ԫ��20Ԫ��������������������ͳ�����ݻ�����ͼ�ٺ�ͼ�������в�������ͳ��ͼ���������ͼ����Ϣ����������⣺
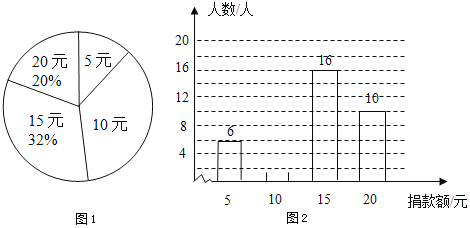
��1��������γ�����ѧ�������������Ϊ5Ԫ��ѧ������ռ���������İٷֱȣ�
��2�����㽫ͼ�ڵ�����ͳ��ͼ����������
��3������У���꼶����Ϊ600�ˣ�������Ƹ�У���꼶һ��������Ԫ��
���𰸡���1�����γ�����ѧ������Ϊ50�ˣ�����Ϊ5Ԫ��ѧ������ռ���������İٷֱ�Ϊ12%����2������������3����У���꼶600�ˣ�һ�����7800Ԫ
��������
��15Ԫ����������ռ�ȱ������������þ��5Ԫ��������������������ռ����.
��������ȥ5Ԫ��15Ԫ��20Ԫ����������10Ԫ��������������ͼ�л���������.
�������Ȩƽ����Ȼ�����600��ɵõ���.
��1��16��32%��50�ˣ�6��50��12%��
�𣺱��γ�����ѧ������Ϊ50�ˣ�����Ϊ5Ԫ��ѧ������ռ���������İٷֱ�Ϊ12%��
��2��50��6��16��10��18�ˣ���ȫ����ͳ��ͼ��ͼ��ʾ��
��3��![]() ��600��7800Ԫ��
��600��7800Ԫ��
�𣺸�У���꼶600�ˣ�һ�����7800Ԫ��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() ������˵��������ǣ� ��
������˵��������ǣ� ��
A.��������x���·�����һԪ���η���![]() ����������ȵ�ʵ����
����������ȵ�ʵ����
B.�������߾���ԭ�㣬��һԪ���η���![]() ����һ��Ϊ0
����һ��Ϊ0
C.��![]() ���������ߵĶԳ������y������
���������ߵĶԳ������y������
D.��![]() ����һԪ���η���
����һԪ���η���![]() ������һ��Ϊ-2
������һ��Ϊ-2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���abc��0����2a+b��0������mΪ����ʵ������a+b��am2+bm����a��b+c��0������ax12+bx1��ax22+bx2����x1��x2����x1+x2��2�����У���ȷ���۵ĸ���Ϊ��������
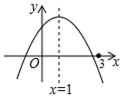
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ���ཻ�ڵ�A(3��0)��
���ཻ�ڵ�A(3��0)��![]() ����
����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ��
��
��1����![]() ��ֵ�͵�
��ֵ�͵�![]() �����ꣻ
�����ꣻ
��2����D(x��y)����������һ�㣬��S��ABD= S��ABC�����![]() ������
������
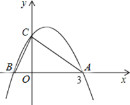
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�DZ߳�Ϊ3�ĵȱ������Σ���BDC�ǵ��������Σ�����BDC��120�㣮��DΪ������һ��60��ǣ�ʹ�����߷ֱ�AB�ڵ�M����AC�ڵ�N������MN������AMN���ܳ�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ӫ�����ϵļס���������ߣ��ɿ����㣩�ֱ�����8cm��A��B����ͬʱ��ʼ���߶�AB�˶����˶������м�����A�ľ���S1��cm����ʱ��t��s���ĺ�����ϵͼ����ͼ2���ҹ�����B�ľ���S2��cm����ʱ��t��s���ĺ�����ϵͼ����ͼ3����֪���ȫ�̵�ƽ���ٶ�Ϊ1.5cm/s������ͼ������P1O1Q1��P2Q2O2������������ȷ���ǣ�������
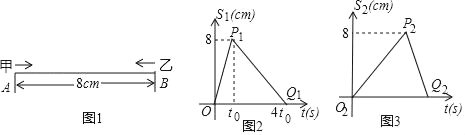
A. ��ߴӵ�A����B���˶��ٶ��Ǵӵ�B����A���˶��ٶȵ�4��
B. �ҹ�ߴӵ�A��B���˶��ٶ�С��1.5cm/s
C. ���������ȫ�̵�ƽ���ٶ�һ��
D. ������������˶������й�����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���ֱ��
�У���ֱ��![]() Ϊ�Գ����������
Ϊ�Գ����������![]() ��ֱ��
��ֱ��![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
��1���������ߵĺ�������ʽ��
��2����ֱ��![]() �������ߵĶԳ���Ľ���Ϊ
�������ߵĶԳ���Ľ���Ϊ![]() ��
��![]() ����������λ�ڶԳ����Ҳ��һ�㣬��
����������λ�ڶԳ����Ҳ��һ�㣬��![]() ����
����![]() ��
��![]() �������ȣ����
�������ȣ����![]() �����ꣻ
�����ꣻ
��3������![]() ��������ֻ��һ��
��������ֻ��һ��![]() ��ʹ
��ʹ![]() ����
����![]() ��ֵ.
��ֵ.
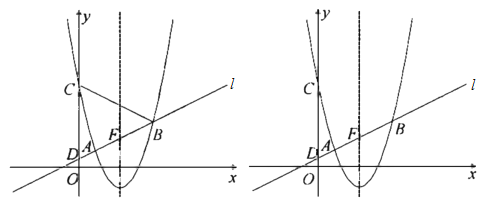
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����![]() x2+bx+c��x�ύ��B��C���㣨��B�ڵ�C����ࣩ����y�ύ�ڵ�A�������ߵĶ���ΪD��B����3��0����A��0��
x2+bx+c��x�ύ��B��C���㣨��B�ڵ�C����ࣩ����y�ύ�ڵ�A�������ߵĶ���ΪD��B����3��0����A��0��![]() ��
��
��1���������߽���ʽ��D�����ꣻ
��2����ͼ1��PΪ�߶�OB�ϣ�����O��B���ᣩһ���㣬����P��y���ƽ���߽��߶�AB�ڵ�M�����������ڵ�N����N��NK��BA��BA�ڵ�K������MNK���MPB��������ʱ����X������һ����Q��ʹ��![]() CQ+QN��Сʱ�����Q�����꼰
CQ+QN��Сʱ�����Q�����꼰![]() CQ+QN��Сֵ��
CQ+QN��Сֵ��
��3����ͼ2���ڣ�2���������£�����ODN������DNƽ�ƣ�ƽ�ƺ�Ķ�Ӧ������Ϊ��O��D��N��������AOC�Ƶ�O��ʱ����ת��A1OC1��λ�ã��ҵ�C1ǡ������AC�ϣ���A1D��N���Ƿ���Ϊ���������Σ��������N�������꣬�����ܣ���˵�����ɣ�
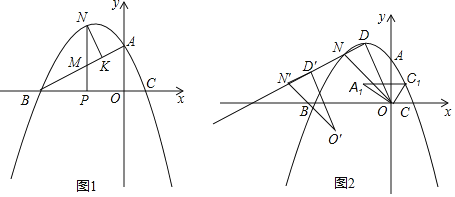
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com