
【题目】如图,四边形ABCD中,∠ADC=∠ABC=90°,连接AC、BD,作DF⊥AC,交AC于点E,交BC于点F,∠ADB=2∠DBC,若BC=![]() ,DF=5
,DF=5![]() ,则AB的长为_____.
,则AB的长为_____.
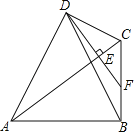
【答案】6![]() .
.
【解析】
作辅助线,根据等腰三角形三线合一的性质得AG=BG,根据矩形的性质和判定证明DN=BG,设DN=a,则AB=2a,证明△FDN∽△ACB,列比例式可表示FN,由勾股定理可得结论.
如图,过D作DG⊥AB于G,DN⊥BC交BC的延长线于N,
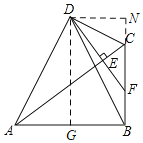
∵∠AGD=∠ABC=90°,
∴DG∥BC,
∴∠DBC=∠BDG,
∵∠ADB=2∠DBC,
∴∠ADG=∠BDG,
∵DG⊥AB,
∴AG=BG,
∵∠N=∠ABC=∠DGB=90°,
∴四边形DGBN是矩形,
∴DN=BG,
设DN=a,则AB=2a,
∵DF⊥AC,
∴∠FEC=∠ACB+∠CFE=90°,
∵∠ACB+∠CAB=90°,
∴∠CFE=∠CAB,
∵∠N=∠ABC=90°,
∴△FDN∽△ACB,
∴![]() ,即
,即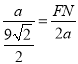 ,
,
FN=![]() ,
,
Rt△DFN中,由勾股定理得:DF2=DN2+FN2,
∴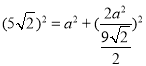 ,
,
设a2=b,
则50=b+![]() ,
,
8b2+81b﹣4050=0,
(b﹣18)(8b+225)=0,
b1=18,b2=﹣![]() (舍),
(舍),
∴a2=18,
∵a>0,
∴a=3![]() ,
,
∴AB=2a=6![]() ,
,
故答案为:6![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
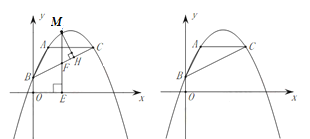
【题目】如图,在平面直角坐标系中,抛物线![]() ,经过点
,经过点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴的平行线交抛物线于另一点
轴的平行线交抛物线于另一点![]() .
.
(1)求抛物线的表达式及其顶点坐标;
(2)如图,点![]() 是第一象限中
是第一象限中![]() 上方抛物线上的一个动点,过点作
上方抛物线上的一个动点,过点作![]() 于点
于点![]() ,作
,作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,在点
,在点![]() 运动的过程中,
运动的过程中,![]() 的周长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
的周长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)如图,连接![]() ,在
,在![]() 轴上取一点
轴上取一点![]() ,使
,使![]() 和
和![]() 相似,请求出符合要求的点
相似,请求出符合要求的点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
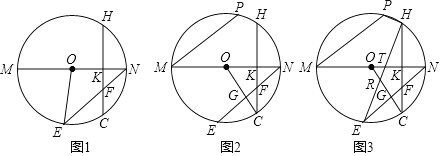
【题目】如图已知:MN为⊙O的直径,点E为弧MC上一点,连接EN交CH于点F,CH是⊙O的一条弦,CH⊥MN于点K.
(1)如图1,连接OE,求证:∠EON=2∠EFC;
(2)如图2,连接OC,OC与NE交于点G,若MP∥EN,MP=2HK,求证:FH=FE;
(3)如图3,在(2)的条件下,连接EH交OC与ON于点R,T,连接PH,若RT:RE=1:5,PH=2![]() ,求OR的长.
,求OR的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
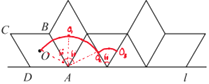
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() ,菱形
,菱形![]() 在直线
在直线![]() 上向右作无滑动的翻滚,每绕着一个顶点旋转
上向右作无滑动的翻滚,每绕着一个顶点旋转![]() 叫一次操作,则经过45次这样的操作菱形中心
叫一次操作,则经过45次这样的操作菱形中心![]() 所经过的路径总长为______.(结果保留
所经过的路径总长为______.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
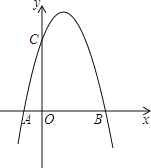
【题目】如图已知在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA.
(1)求点A坐标;
(2)求这条抛物线的解析式,并求出它的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
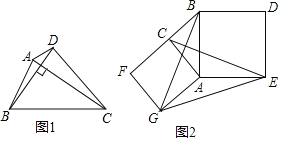
【题目】概念理解:对角线互相垂直的四边形叫做垂美四边形
(1)性质探究:如图1,四边形ABCD是垂美四边形,直接写出AB2、CD2、AD2、BC2的数量关系: .
(2)解决问题:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.若AC=4,AB=5,求GE的长(可直接利用(1)中性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=a![]() +bx+c的对称轴是直线x=1,且过点(1,0).顶点位于第二象限,其部分图象如图所示,给出以下判断:①ab
+bx+c的对称轴是直线x=1,且过点(1,0).顶点位于第二象限,其部分图象如图所示,给出以下判断:①ab![]() ;② 4a-2b+c
;② 4a-2b+c![]() ;③8a+c
;③8a+c![]() ;④c=3a-3b;
;④c=3a-3b;
⑤直线y=2x+2与抛物线y=a![]() +bx+c两个交点的横坐标分别为
+bx+c两个交点的横坐标分别为![]() ,则
,则![]() =5.
=5.
其中正确的个数有( )
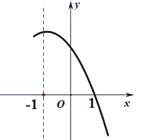
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
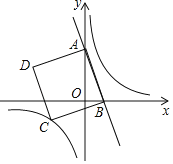
【题目】如图,直线y=﹣3x+3与y轴交于点A,与x轴交于点B,以线段AB为边,在线段AB的左侧作正方形ABCD,点C在反比例函数y=![]() (k≠0)的图象上,当正方形ABCD沿x轴正方向向右平移_____个单位长度时,正方形ABCD的一个顶点恰好落在该反比例函数图象上.
(k≠0)的图象上,当正方形ABCD沿x轴正方向向右平移_____个单位长度时,正方形ABCD的一个顶点恰好落在该反比例函数图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com