
【题目】抛物线y=a![]() +bx+c的对称轴是直线x=1,且过点(1,0).顶点位于第二象限,其部分图象如图所示,给出以下判断:①ab
+bx+c的对称轴是直线x=1,且过点(1,0).顶点位于第二象限,其部分图象如图所示,给出以下判断:①ab![]() ;② 4a-2b+c
;② 4a-2b+c![]() ;③8a+c
;③8a+c![]() ;④c=3a-3b;
;④c=3a-3b;
⑤直线y=2x+2与抛物线y=a![]() +bx+c两个交点的横坐标分别为
+bx+c两个交点的横坐标分别为![]() ,则
,则![]() =5.
=5.
其中正确的个数有( )
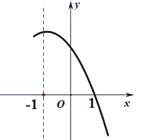
A.5个B.4个C.3个D.2个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
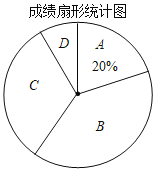
【题目】在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
成绩频数分布统计表
组别 | A | B | C | D |
成绩x(分) | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
人数 | 10 | m | 16 | 4 |
请观察上面的图表,解答下列问题:
(1)统计表中m= ,D组的圆心角为 °;
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
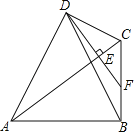
【题目】如图,四边形ABCD中,∠ADC=∠ABC=90°,连接AC、BD,作DF⊥AC,交AC于点E,交BC于点F,∠ADB=2∠DBC,若BC=![]() ,DF=5
,DF=5![]() ,则AB的长为_____.
,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
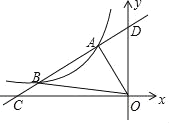
【题目】如图,直线y=kx+b与反比例函数![]() 的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.
的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.
(1)求此一次函数和反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
情景再现
我们动手操作:把正方形ABCD,从对角线剪开就分剪出两个等腰直角三角形,把其中一个等腰三角形与正方形ABCD重新组合在一起,图形变得丰富起来,当图形旋转时问题也随旋转应运而生.
如图①把正方形ABCD沿对角线剪开,得两个等腰直角三角形△ACD和△BCE,
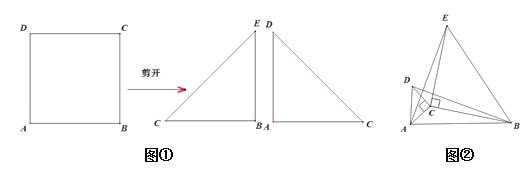
(1)问题呈现
我们把剪下的两个三角形一个放大另一个缩小拼成如图②所示
①点P是一动点,若AB=3,PA=1,当点P位于_ __时,线段PB的值最小;若AB=3,PA=5,当点P位于__ _时,线段PB有最大值.PB的最大值和最小值分别是______.
②直接写出线段AE与DB的关系是_ ________.
(2)我们把剪下的其中一个三角形放大与正方形组合如图③所示,点E在直线BC上,FM⊥CD交直线CD于M.
①当点E在BC上时,通过观察、思考易证:AD=MF+CE;
②当点E在BC的延长线时,如图④所示;
当点E在CB的延长线上时,如图⑤所示,
线段AD、MF、CE具有怎样的数量关系?写出你的猜想,并选择图④或图⑤证明你的猜想.
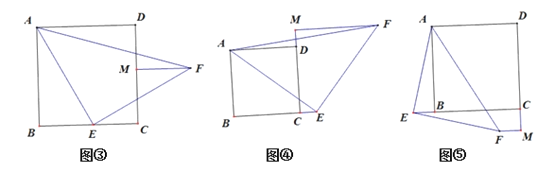
问题拓展
(3)连接EM,当![]() =8,
=8,![]() =50,其他条件不变,直接写出线段CE的长_______.
=50,其他条件不变,直接写出线段CE的长_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】横、纵坐标均为整数的点叫做格点,例如A(1,4),B(1,1),C(4,1),D(4,4),E(2,1)都是格点.
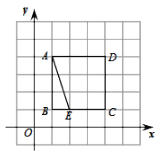
(1)取格点F,使得BF⊥AE,BF=AE;
(2)将线段BF绕点F顺时针旋转90°,得到线段FM;
(3)用无刻度的直尺在AD上取点N,使得FN=CF+AN,保留作图痕迹,并直接写出点F,M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b交x轴于点A(1,0) ,与双曲线![]() 交于点
交于点![]()
(1)求直线AB的解析式为____ ____________;
(2)若 x 轴上存在动点 M(m,0),过点 M 且与 x 轴垂直的直线与直线AB交于点C,与双曲线交于点D(C、D两点不重合),当BC >BD时,写出m的取值范围_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈
,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈![]() ,cos53°≈0.60)
,cos53°≈0.60)
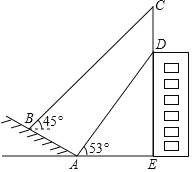
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com