
【题目】概念理解:对角线互相垂直的四边形叫做垂美四边形
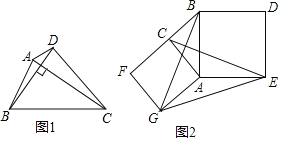
(1)性质探究:如图1,四边形ABCD是垂美四边形,直接写出AB2、CD2、AD2、BC2的数量关系: .
(2)解决问题:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.若AC=4,AB=5,求GE的长(可直接利用(1)中性质)
【答案】(1)AD2+BC2=AB2+CD2;(2)GE=![]() .
.
【解析】
(1)利用勾股定理即可得出结论;
(2)先判断出CE⊥BG,得出四边形CGEB是垂美四边形,借助(1)的结论即可得出结论.
(1)结论:AD2+BC2=AB2+CD2,
如图1中,设BD交AC于E.

∵AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2;
故答案为:AD2+BC2=AB2+CD2.
(2)连接CG、BE,
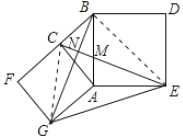
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,
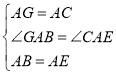 ,
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,
又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=3,CG=4![]() ,BE=5
,BE=5![]() ,
,
∴GE2=CG2+BE2﹣CB2=73,
∴GE=![]() .
.


科目:初中数学 来源: 题型:
【题目】哈市某中学为了丰富校园文化生活.校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查。将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
(1)通过计算补全条形统计图;
(2)在这次调查中,一共抽取了多少名学生?
(3)如果全校有680名学生,请你估计这680名学生中参加演讲比赛的学生有多少名?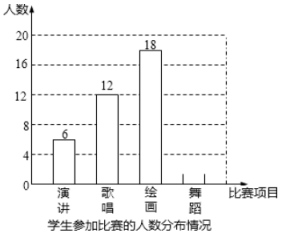
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国的经济总量已居世界第二,人民富裕了,有的家庭拥有多种车型.小红家有A、B、C三种车型,已知3辆A型车的载重量与4辆B型车的载重量之和刚好等于2辆C型车的载重量;4辆B型车的载重量与1辆C型车的载重量之和刚好等于6辆A型车的载重量.现有一批货物,原计划用C型车10次可全部运完,由于C型车另有运输任务,现在安排A型车单独装运12次,余下的货物由B型车单独装运刚好可以全部运完,则B型车需单独装运_____次(每辆车每次都满载重量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条笔直的公路![]() 穿过草原,公路边有一卫生站
穿过草原,公路边有一卫生站![]() 距公路
距公路![]() 的地方有一居民点
的地方有一居民点![]() ,
,![]() 、
、![]() 之间的距离为
之间的距离为![]() .一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是
.一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是![]() ,在草地上行驶的最快速度是
,在草地上行驶的最快速度是![]() .问司机应在公路上行驶多少千米?全部所用的行车时间最短?最短时间为多少?
.问司机应在公路上行驶多少千米?全部所用的行车时间最短?最短时间为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
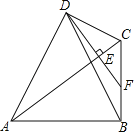
【题目】如图,四边形ABCD中,∠ADC=∠ABC=90°,连接AC、BD,作DF⊥AC,交AC于点E,交BC于点F,∠ADB=2∠DBC,若BC=![]() ,DF=5
,DF=5![]() ,则AB的长为_____.
,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图②所示,则图②中的b等于( )

A. ![]() B.
B. ![]() C. 5D. 4
C. 5D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
情景再现
我们动手操作:把正方形ABCD,从对角线剪开就分剪出两个等腰直角三角形,把其中一个等腰三角形与正方形ABCD重新组合在一起,图形变得丰富起来,当图形旋转时问题也随旋转应运而生.
如图①把正方形ABCD沿对角线剪开,得两个等腰直角三角形△ACD和△BCE,
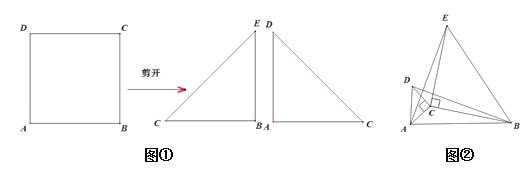
(1)问题呈现
我们把剪下的两个三角形一个放大另一个缩小拼成如图②所示
①点P是一动点,若AB=3,PA=1,当点P位于_ __时,线段PB的值最小;若AB=3,PA=5,当点P位于__ _时,线段PB有最大值.PB的最大值和最小值分别是______.
②直接写出线段AE与DB的关系是_ ________.
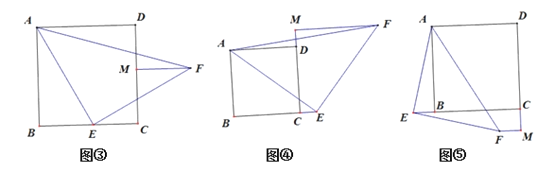
(2)我们把剪下的其中一个三角形放大与正方形组合如图③所示,点E在直线BC上,FM⊥CD交直线CD于M.
①当点E在BC上时,通过观察、思考易证:AD=MF+CE;
②当点E在BC的延长线时,如图④所示;
当点E在CB的延长线上时,如图⑤所示,
线段AD、MF、CE具有怎样的数量关系?写出你的猜想,并选择图④或图⑤证明你的猜想.
问题拓展
(3)连接EM,当![]() =8,
=8,![]() =50,其他条件不变,直接写出线段CE的长_______.
=50,其他条件不变,直接写出线段CE的长_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
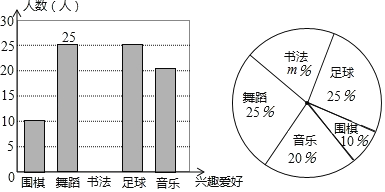
![]() 学校这次调查共抽取了 名学生;
学校这次调查共抽取了 名学生;
![]() 求
求![]() 的值并补全条形统计图;
的值并补全条形统计图;
![]() 在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
![]() 设该校共有学生
设该校共有学生![]() 名,请你估计该校有多少名学生喜欢足球.
名,请你估计该校有多少名学生喜欢足球.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com