
【题目】某校初三年级有四个班,每班挑选乒乓球男女队员各一人,组成年级混合双打代表队,那么四对混合双打中,没有一队选手是同班同学的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
首先根据乘法公式,求得4男4女组成四队混合双打的情况共有24种,然后设一、二、三、四班的男、女选手分别为A1、B1、A2、B2、A3、B3、A4、B4,则可列出四队混合双打中,没有一对选手是同班同学的情况,再根据概率公式,即可求得答案.
解:∵先把四个女运动员任意排列,设为A B C D,
和A配合的男运动员有4个选择;
和B配合的男运动员剩下3种选择;
和C配合的男运动员剩下2种选择;
最后一个和D配合.
所以总共有24种.
∴4男4女组成四队混合双打的情况共有:4×3×2=24种,
设一、二、三、四班的男、女选手分别为A1、B1、A2、B2、A3、B3、A4、B4,则四队混合双打中,没有一对选手是同班同学的情景如下:
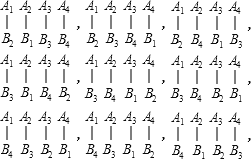
由上得共有9种情形.
故四对混合双打中,没有一对选手是同班同学的概率是:![]() .
.
故选C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一项工程,甲队单独完成比乙队单独完成少用8天,甲队单独做3天的工作乙队单独做需要5天.
(1)甲、乙两队单独完成此项工程各需几天?
(2)甲队每施工一天则需付给甲队工程款5.5万元,乙队每施工一天则需付给乙队工程款3万元.该工程先由甲、乙两队合作若干天后,再由乙队完成剩下的工程.若要求完成此项工程的工程款不超过65万元,则甲、乙两队最多合作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ACB=90°,AC>BC,分别以△ABC的边AB,BC,CA为一边向△ABC外作正方形ABDE,正方形BCMN,正方形CAFG,连接EF,GM,设△AEF,△CGM的面积分别为S1,S2,则下列结论正确的是( )
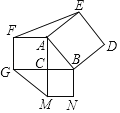
A.S1=S2B.S1<S2C.S1>S2D.S1≤S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( )
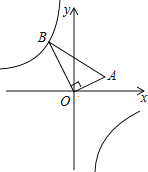
A.﹣2B.﹣4C.4D.﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销A、B两种商品,现有如下信息:
信息1:A、B两种商品的进货单价之和是3元;
信息2:A商品零售单价比进货单价多1元,B商品零售单价比进货单价的2倍少1元;
信息3:按零售单价购买A商品3件和B商品2件,共付12元.
请根据以上信息,解答下列问题:
(1)求A、B两种商品的零售单价;
(2)该商店平均每天卖出A商品500件和B商品1500件.经调查发现,A种商品零售单价每降0.1元,A种商品每天可多销售100件.商店决定把A商品的零售单价下降m(m>0)元,B商品的零售单价和销量都不变,在不考虑其他因素的条件下,当m为多少时,商品每天销售A、B两种商品获取的总利润为2000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题:
材料一:我们将![]() 与
与![]() 称为一对“对偶式”因为
称为一对“对偶式”因为![]() ,所以构造“对俩式”相乘可以有效地将
,所以构造“对俩式”相乘可以有效地将![]() 和
和![]() 中的
中的![]() 去掉.例如:已知
去掉.例如:已知![]() ,求
,求![]()
![]() 的值.解:
的值.解:![]() ,
,![]()
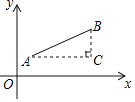
材料二:如图,点![]() ,点
,点![]() ,以AB为斜边作
,以AB为斜边作![]() ,则
,则![]() ,于是
,于是![]() ,
,![]() ,所以
,所以![]() .反之,可将代数式
.反之,可将代数式![]() 的值看作点
的值看作点![]() 到点
到点![]() 的距离.
的距离.
例如:![]() =
=![]() .
.
所以可将代数式![]() 的值看作点
的值看作点![]() 到点
到点![]() 的距离.
的距离.
![]() 利用材料一,解关于x的方程:
利用材料一,解关于x的方程:![]() ,其中
,其中![]() ;
;
![]() 利用材料二,求代数式
利用材料二,求代数式![]() 的最小值,并求出此时y与x的函数关系式,写出x的取值范图;
的最小值,并求出此时y与x的函数关系式,写出x的取值范图;
![]() 将
将![]() 所得的y与x的函数关系式和x的取值范围代入
所得的y与x的函数关系式和x的取值范围代入![]() 中解出x,直接写出x的值.
中解出x,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
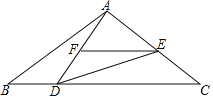
【题目】如图:已知在△ABC中,AB=AC,点D是BC上一点,∠ADE=∠B,
(1)求证:△ABD~△DCE;
(2)点F在AD上,且![]() =
=![]() ,求证:EF∥CD.
,求证:EF∥CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y1=-x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点
交于点A(1,m),这两条直线分别与x轴交于B,C两点
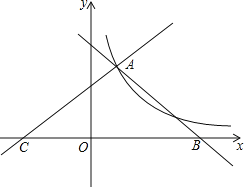
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形 ABCD 中,M,N,P,Q 分别为边 AB,BC,CD,DA 上的点(不与端点重合).对于任意矩形 ABCD,下面四个结论中:①存在无数个四边形 MNPQ 是平行四边形;②存在无数个四边形 MNPQ 是矩形;③存在无数个四边形 MNPQ 是菱形;④不存在四边形 MNPQ 是正方形.所有正确结论的序号是_________________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com