
【题目】如图,△ABC 中,AB=AC,以 AB 为直径的⊙O 与 BC 相交于点 D, 与 CA 的延长线相交于点 E,过点 D 作 DF⊥AC 于点 F.
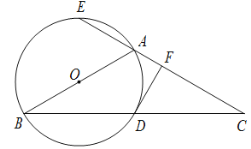
(1)试说明 DF 是⊙O 的切线;
(2)①当∠C= °时,四边形 AODF 为矩形;
②当 tanC= 时,AC=3AE.
【答案】(1)见解析;(2)①45°;②![]()
【解析】
(1)由等腰三角形的性质可证∠ODB=∠C,从而OD//AC,可证OD⊥DF,即可解决问题;
(2)①当∠B=45°时,四边形ODEC是正方形,由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论;
②直接利用锐角三角函数关系得出BC的长,再利用直角三角形的性质得出DE的长.
解:(1)证明:连接OD,
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD//AC,
∵DF⊥AC,
∴OD⊥DF,点D在⊙O上,
∴DF是⊙O的切线;
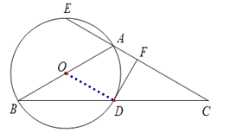
(2)45°,理由如下:
∵AB=AC,
∴∠ABC=∠C=45°,
∴∠BAC=90°,
∵∠ODF=∠AFD=90°,
∴四边形AODF为矩形;
(3)![]() ,理由如下,
,理由如下,
连接BE,
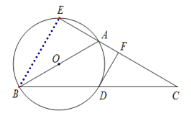
∵AB是直径,
∴∠AEB=90°,
∵AB=AC,AC=3AE,
∴AB=3AE,CE=4AE,
∴BE2=AB2-AE2 =8AE2,
即BE=![]() AE,
AE,
在Rt△BEC中,tanC=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则△BCN的面积是( )
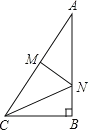
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲队单独完成比乙队单独完成少用8天,甲队单独做3天的工作乙队单独做需要5天.
(1)甲、乙两队单独完成此项工程各需几天?
(2)甲队每施工一天则需付给甲队工程款5.5万元,乙队每施工一天则需付给乙队工程款3万元.该工程先由甲、乙两队合作若干天后,再由乙队完成剩下的工程.若要求完成此项工程的工程款不超过65万元,则甲、乙两队最多合作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
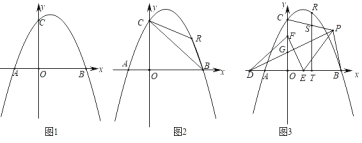
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 边长是定值,点
边长是定值,点![]() 是它的外心,过点
是它的外心,过点![]() 任意作一条直线分别交
任意作一条直线分别交![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 折叠,得到
折叠,得到![]() ,若
,若![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() ,则下列判断错误的是( )
,则下列判断错误的是( )
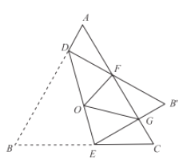
A.△![]() ≌△
≌△![]()
B.![]() 的周长是一个定值
的周长是一个定值
C.四边形![]() 的面积是一个定值
的面积是一个定值
D.四边形![]() 的面积是一个定值
的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ACB=90°,AC>BC,分别以△ABC的边AB,BC,CA为一边向△ABC外作正方形ABDE,正方形BCMN,正方形CAFG,连接EF,GM,设△AEF,△CGM的面积分别为S1,S2,则下列结论正确的是( )
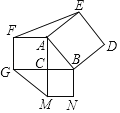
A.S1=S2B.S1<S2C.S1>S2D.S1≤S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( )
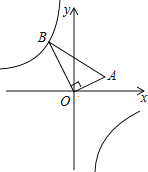
A.﹣2B.﹣4C.4D.﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y1=-x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点
交于点A(1,m),这两条直线分别与x轴交于B,C两点
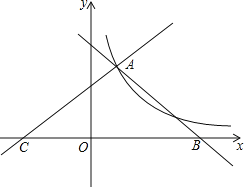
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,求此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com