
����Ŀ��ij��˾����һ�ֽ���Ϊ20Ԫ/���ļ���������������y������������ۼ۸�x��Ԫ/�����ı仯���±���
�۸�x��Ԫ/���� | �� | 30 | 40 | 50 | 60 | �� |
������y������� | �� | 5 | 4 | 3 | 2 | �� |
ͬʱ�����۹����е�������֧���������ۣ��ܼ�40��Ԫ��
��1���۲첢�������е�y��x֮��Ķ�Ӧ��ϵ������ѧ����һ�κ�������������������κ������й�֪ʶд��y���������x��Ԫ/�����ĺ�������ʽ��
��2������ù�˾�������ּ������ľ�������z����Ԫ�������ۼ۸�x��Ԫ/�����ĺ�������ʽ�����ۼ۸�Ϊ����Ԫʱ��������������ֵ�Ƕ��٣�
��3���ù�˾Ҫ�������ܵ���40��Ԫ����д�����ۼ۸�x��Ԫ/������ȡֵ��Χ�������迼�������������ܴ����ۼ۸�Ӧ��Ϊ����Ԫ��
���𰸡���1�� y=![]() x+8
x+8
��2�� z=![]() x2+10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ
x2+10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ
��3��40��x��60�����ۼ۸�Ӧ��Ϊ40Ԫ/��
��������
��1���������ݵó�y��x��һ�κ�����ϵ���������ô���ϵ������һ�κ�������ʽ��
��2������z=��x��20��y��40�ó�z��x�ĺ�����ϵʽ��Ӧ�ö��κ�����ֵԭ����⼴�ɣ�
��3���������40=![]() ��x��50��2+50ʱx��ֵ���Ӷ����κ��������ʸ��ݵó�x��Ԫ/������ȡֵ��Χ�����һ�κ��������ʼ�����ý����
��x��50��2+50ʱx��ֵ���Ӷ����κ��������ʸ��ݵó�x��Ԫ/������ȡֵ��Χ�����һ�κ��������ʼ�����ý����
�⣺��1�����ݱ��������ݿɵó���y��x��һ�κ�����ϵ�������ʽΪ��y=ax+b��
��![]() ����ã�
����ã�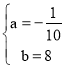 ��
��
�ຯ������ʽΪ��y=![]() x+8��
x+8��
��2����������ã�
z=��x��20��y��40=��x��20����![]() x+8����40=
x+8����40=![]() x2+10x��200=
x2+10x��200=![]() ��x2��100x����200
��x2��100x����200
=![]() [��x��50��2��2500]��200=
[��x��50��2��2500]��200=![]() ��x��50��2+50��
��x��50��2+50��
��![]() ��0����x=50��z���=50��
��0����x=50��z���=50��
��ù�˾�������ּ������ľ�������z�����ۼ۸�x�ĺ�������ʽΪz=![]() x2+10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ��
x2+10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ��
��3������˾Ҫ������Ϊ40��Ԫʱ����![]() ��x��50��2+50=40����ã�x1=40��x2=60��
��x��50��2+50=40����ã�x1=40��x2=60��
������ͼ��IJ�ͼ��
ͨ���۲캯��y=![]() ��x��50��2+50��ͼ��֪���չ�˾Ҫ��ʹ����������40��Ԫ�������ۼ۸��ȡֵ��ΧΪ��40��x��60��
��x��50��2+50��ͼ��֪���չ�˾Ҫ��ʹ����������40��Ԫ�������ۼ۸��ȡֵ��ΧΪ��40��x��60��
��y��x�ĺ�����ϵʽΪ��y=![]() x+8��y��x����������٣�
x+8��y��x����������٣�
�������迼�������������ܴ����ۼ۸�Ӧ��Ϊ40Ԫ/����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
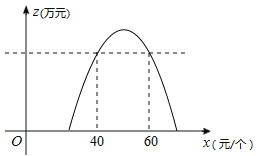
����Ŀ����ͼ����֪�ڡ�ABC�У�AB��AC����D��BC��һ�㣬��ADE����B��
��1����֤����ABD����DCE��
��2����F��AD�ϣ���![]() ��
��![]() ����֤��EF��CD��
����֤��EF��CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��(a2+1)x2+bx+c������A����3��t����B��4��t�����㣬��ʽ(a2+1)��x-2)2+bx<2b-c+t�Ľ⼯��_____________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ��� ABCD �У�M��N��P��Q �ֱ�Ϊ�� AB��BC��CD��DA �ϵĵ㣨����˵��غϣ�������������� ABCD�������ĸ������У��ٴ����������ı��� MNPQ ��ƽ���ı��Σ��ڴ����������ı��� MNPQ �Ǿ��Σ��۴����������ı��� MNPQ �����Σ��ܲ������ı��� MNPQ �������Σ�������ȷ���۵������_________________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�� xOy �У����ڡ�C����C��һ�� P���������¶��壺�����ڹ��� P ��ֱ�� l��ʹ�������C �ཻ���صõ��ҳ�Ϊ![]() ����Ƶ� P Ϊ��C�ġ�k-���ڵ㡱��
����Ƶ� P Ϊ��C�ġ�k-���ڵ㡱��
��1����֪��O�İ뾶Ϊ 4��
���ڵ���![]() ����O�ġ�4-���ڵ㡱��______________��
����O�ġ�4-���ڵ㡱��______________��
�ڵ� P ��ֱ��y=![]() x�ϣ����� P Ϊ��O�ġ�4-���ڵ㡱����� P ��������y��ȡֵ��Χ��____________��
x�ϣ����� P Ϊ��O�ġ�4-���ڵ㡱����� P ��������y��ȡֵ��Χ��____________��
��2����C��Բ��Ϊ��-1��0�����뾶Ϊ 3��ֱ��![]() x �ᣬy ��ֱ��� M��N�����߶� MN �ϴ��ڡ�C�� ��2
x �ᣬy ��ֱ��� M��N�����߶� MN �ϴ��ڡ�C�� ��2![]() -���ڵ㡱���� b ��ȡֵ��Χ��____________��
-���ڵ㡱���� b ��ȡֵ��Χ��____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�CA��CB��AB��![]() ��CD��AB�ڵ�D��CD��5����O�͵�E���߶�CD�ϣ�ED��1����P�ڱ�AB�ϣ���EΪԲ�ģ�EPΪ�뾶��Բ��AB�ߵ���һ������Ϊ��Q����P�ڵ�Q����ࣩ����OΪԲ�ģ�OCΪ�뾶��ԲOǡ�þ���P��Q���㣬����CP�����߶�AP�ij���Ϊx��
��CD��AB�ڵ�D��CD��5����O�͵�E���߶�CD�ϣ�ED��1����P�ڱ�AB�ϣ���EΪԲ�ģ�EPΪ�뾶��Բ��AB�ߵ���һ������Ϊ��Q����P�ڵ�Q����ࣩ����OΪԲ�ģ�OCΪ�뾶��ԲOǡ�þ���P��Q���㣬����CP�����߶�AP�ij���Ϊx��
��1����ԲEǡ�þ�����Oʱ����ԲE�İ뾶��
��2������CQ�����PCQ������ֵΪy����y��x�ĺ�����ϵʽ��������
��3������PED��3��PCE����S��PCQ��ֵ��
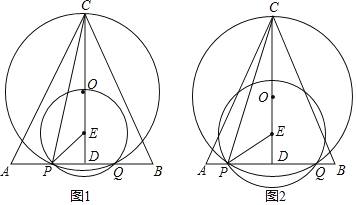
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���BCD=��D=90����E�DZ�AB���е�.��֪AD=1��AB=2.
��1����BC=x��CD=y����y����x�ĺ�����ϵʽ����д��������
��2������B=70��ʱ�����AEC�Ķ�����
��3������ACEΪֱ��������ʱ�����BC�ij�.
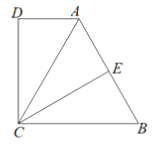
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ֱ������ϵ�У���֪��A��1��0����B��0����2�������߶�AB�Ƶ�A����ʱ�뷽����ת90����AC����������y=��![]() x2+bx+2������C��
x2+bx+2������C��
��1���������ߵĽ���ʽ��
��2����ͼ����������ƽ�ƣ���������ԭ��ʱ����Q��0����2������ƽ����x���ֱ�߽���������E��F���㣬����y������������Ƿ����һ��P��ʹ��PEF��������y���ϣ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�
��3�������������Ƿ����һ��M��ʹ����MΪԲ�ģ���![]() Ϊ�뾶��Բ��ֱ��BC���У������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
Ϊ�뾶��Բ��ֱ��BC���У������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
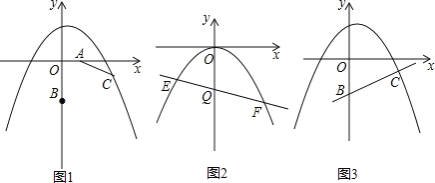
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������![]() ��x����A��C���㣬��y���ڵ�B����OB=2CO.
��x����A��C���㣬��y���ڵ�B����OB=2CO.
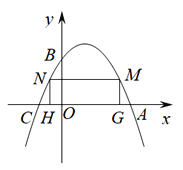
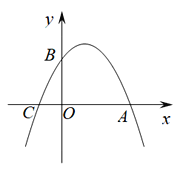
(1)����κ�������ʽ��
(2)�ڶ��κ���ͼ��λ��x���Ϸ���������������M��N���ҵ�N�ڵ�M����࣬��M��N��x��Ĵ��߽�x���ڵ�G��H���㣬���ı���MNHGΪ����ʱ����þ����ܳ������ֵ��
(3) �����߶Գ������Ƿ���ڵ�P��ʹ�á�ABPΪֱ�������Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com