
【题目】如图,二次函数y=ax2+bx(a≠0)的图象经过点A(1,4),对称轴是直线x=﹣![]() ,线段AD平行于x轴,交抛物线于点D,在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
,线段AD平行于x轴,交抛物线于点D,在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
(1)求该二次函数的解析式;
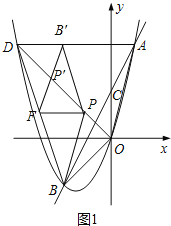
(2)设点F是BD的中点,点P是线段DO上的动点,将△BPF沿边PF翻折,得到△B′PF,使△B′PF与△DPF重叠部分的面积是△BDP的面积的![]() ,若点B′在OD上方,求线段PD的长度;
,若点B′在OD上方,求线段PD的长度;
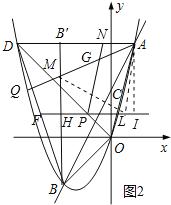
(3)在(2)的条件下,过B′作B′H⊥PF于H,点Q在OD下方的抛物线上,连接AQ与B′H交于点M,点G在线段AM上,使∠HPN+∠DAQ=135°,延长PG交AD于N.若AN+B′M=![]() ,求点Q的坐标.
,求点Q的坐标.
【答案】(1)y=x2+3x;(2)PD=3![]() ;(3)Q(﹣
;(3)Q(﹣![]() ,
,![]() ).
).
【解析】
(1)根据二次函数y=ax2+bx(a≠0)的图象经过点A(1,4),对称轴是直线x=﹣![]() ,列出方程组即可解决问题.
,列出方程组即可解决问题.
(2)如图1中,首先求出直线AC与抛物线的交点B坐标,再证明DP′=PP′,推出四边形BFB′P是菱形,在RT△POB中求出OP即可解决问题.
(3)如图2中,过A作AI⊥HP,可得四边形AB′HI是正方形,过A作AL∥PN,连接ML,在Rt△MHL中,由ML2=MH2+HL2列出方程即可解决问题.
解:(1)由题意得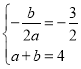 ,解得
,解得![]() ,
,
![]() 二次函数的解析式为
二次函数的解析式为![]() ;
;
(2)如图1中,![]() ,
,![]() ,
,
设直线![]() 解析式为
解析式为![]() ,则
,则![]() ,
,
解得![]() .
.
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
由![]() 解得
解得![]() 或
或![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,
![]() 在
在![]() 上,
上,![]() ,
,
在![]() 中,
中,![]() ,
,
![]()
![]() ;
;
(3)如图2中,由(2)得![]() ,
,![]() ’
’ ![]() .
.
过![]() 作
作![]() ,可得四边形
,可得四边形![]() 是正方形,过
是正方形,过![]() 作
作![]() ,连接
,连接![]() .
.
由![]() 得
得![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
解得![]() ,
,
![]() ,
,
![]() 直线
直线![]() 解析式为:
解析式为:![]() ,
,
由 解得
解得![]() 或
或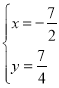 ,
,
![]() ,
,![]() .
.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】在如图的直角坐标系中,已知点A(1,0)、B(0,﹣2),将线段AB绕点A按逆时针方向旋转90°至AC,若抛物线y=﹣![]() x2+bx+2经过点C.
x2+bx+2经过点C.
(1)求抛物线的解析式;
(2)如图,将抛物线平移,当顶点至原点时,过Q(0,﹣2)作不平行于x轴的直线交抛物线于E、F两点,问在y轴的正半轴上是否存在一点P,使△PEF的内心在y轴上?若存在,求出点P的坐标;若不存在,说明理由.
(3)在抛物线上是否存在一点M,使得以M为圆心,以![]() 为半径的圆与直线BC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
为半径的圆与直线BC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线![]() 交x轴于A,C两点,交y轴于点B,且OB=2CO.
交x轴于A,C两点,交y轴于点B,且OB=2CO.
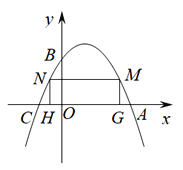
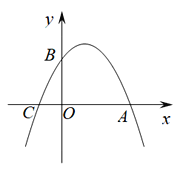
(1)求二次函数解析式;
(2)在二次函数图象位于x轴上方部分有两个动点M、N,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;
(3) 抛物线对称轴上是否存在点P,使得△ABP为直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销的一种产品每件成本为40元,要求在90天内完成销售任务.已知该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
x+50 | 90 |
任务完成后,统计发现销售员小王90天内日销售量p(件)与时间(第x天)满足一次函数关系p=﹣2x+200.设小王第x天销售利润为W元.
(1)直接写出W与x之间的函数关系式,井注明自变量x的取值范围;
(2)求小生第几天的销售量最大?最大利润是多少?
(3)任务完成后,统计发现平均每个销售员每天销售利润为4800公司制定如下奖励制度:如果一个销售员某天的销售利润超过该平均值,则该销售员当天可获得200元奖金.请计算小王一共可获得多少元奖金?
查看答案和解析>>
科目:初中数学 来源: 题型:
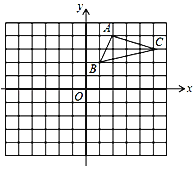
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1(点A的对应点为A1,点B的对应点为B1,点C的对应点为C1),并写出点A1的坐标;
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2(点A1的对应点为A2,点B1的对应点为B2,点C1的对应点为C2).
查看答案和解析>>
科目:初中数学 来源: 题型:
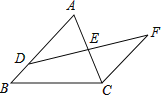
【题目】如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.
(1)求证:AD=CF.
(2)连接AF,CD,求证:四边形ADCF为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
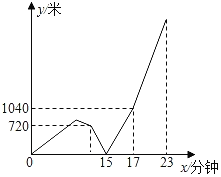
【题目】小刚从家出发匀速步行去学校上学.几分钟后发现忘带数学作业,于是掉头原速返回并立即打电话给爸爸,挂断电话后爸爸立即匀速跑步去追小刚,同时小刚以原速的两倍匀速跑步回家,爸爸追上小刚后以原速的![]() 倍原路步行回家.由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校,并在从家出发后23分钟到校(小刚被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小刚从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小刚家到学校的路程为_____米.
倍原路步行回家.由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校,并在从家出发后23分钟到校(小刚被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小刚从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小刚家到学校的路程为_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com